You are here: Vanderbilt Biostatistics Wiki>Main Web>Projects>MicroArrayMassSpec>GeneralWfccmDesign>WfccmClassDescriptions>WfccmAlgorithmInfo (21 Jan 2005, WillGray)Edit Attach
Info Algorithm
Performed on an ordered (ascending) set of numbers and labels of size N. There must be only 2 unique labels (Label 1 and label 2).
Seperate the list into N - 1 grouping sets such that:| Set | Left | Right |
| 1 | |
|
| 2 | |
|
| |
|
|
| N-1 | |
|
-
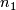 : the number of values in group 1
: the number of values in group 1
-
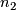 : the number of values in group 2
: the number of values in group 2
- a: Percent of values on the left side.
- 1 - a: Percent of values on the right side.
- b: Percent of left side that is label 1.
- 1 - b: Percent of left side that is label 2.
- c: Percent of right side that is label 1.
- 1 - c: Percent of right side that is label 2.
- Entropy:
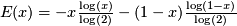 ,
, 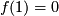 ,
, 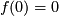
- Info:
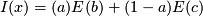
Choose the smallest Info value as the final info value.
Sorting: Sort first by value (ascending), then by labels (ascending). Duplicate values: Calculate the info_n for the section that has duplicates. Then reorder the section by sorting labels(desc) and calculate the interior of the duplicate section (of size duplicateN 1) again. Do the same for all sections that have duplicates.Examples:
Example 1
grouping 1 2 1 1 2 ordered 1 1 2 1 2 values 1 8 3 7 5 1 3 5 7 8 5 values so there will be 4 cut points 1 1 2 1 2 a=1/5 b=1/1 c=2/4 entropy(b)= 0 entropy(c)= 1 info = 0.8000 1 1 2 1 2 a=2/5 b=2/2 c=1/3 entropy(b)= 0 entropy(c)= 0.9183 info = 0.5510 1 1 2 1 2 a=3/5 b=2/3 c=1/2 entropy(b)= 0.9183 entropy(c)= 1 info = 0.9510 1 1 2 1 2 a=4/5 b=3/4 c=0/1 entropy(b)= 0.8113 entropy(c)= 0 info = .6490 The smallest value is 0.5510
Example 2
grouping 1 2 2 1 1 ordered 1 2 1 1 2 values 1 8 5 8 8 1 5 8 8 8 5 values so there will be 4 cut points 1 2 1 1 2 1 5 8 8 8 a=1/5 b=1/1 c=2/4 entropy(b)= 0 entropy(c)= 1 info =0.8 -- Info won't change if we reorder the the duplicate by group (desc) 1 2 1 1 2 1 5 8 8 8 a=2/5 b=1/2 c=2/3 entropy(b)= 1 entropy(c)= 0.9183 info = 0.9510 -- Duplicate section first run 1 2 1 1 2 1 5 8 8 8 a=3/5 b=2/3 c=1/2 entropy(b)= 0.9183 entropy(c)= 1 info = 0.9510 1 2 1 1 2 1 5 8 8 8 a=4/5 b=3/4 c=0/1 entropy(b)= 0.8113 entropy(c)= 0 info = .6490 -- Duplicate section second run. Reordered by group(desc) 1 2 2 1 1 1 5 8 8 8 a=3/5 b=1/3 c=2/2 entropy(b)= 0.9183 entropy(c)= 0 info = 0.5510 1 2 2 1 1 1 5 8 8 8 a=4/5 b=2/4 c=1/1 entropy(b)= 1 entropy(c)= 0 info = 0.8000 The smallest value is 0.5510
Edit | Attach | Print version | History: r4 < r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r4 - 21 Jan 2005, WillGray
 Copyright &© 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright &© 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Vanderbilt Biostatistics Wiki? Send feedback