You are here: Vanderbilt Biostatistics Wiki>Main Web>MethodsDisc>DataAnalysisDisc (12 Apr 2010, RobertGreevy)Edit Attach
General Data Analysis Discussion Board
Discussions related to Rafe Donahue's 11Oct06 seminar in the Department
FrankHarrell's comments
Rafe's excellent seminar yesterday addressed a large number of important issues. Just to continue the excellent dialog started by Rafe I wanted to offer a few thoughts. Comments welcomed.- Often times graphical summaries are the best final results of an analysis and no modeling is needed. For these times, in-depth looks at the data without translating to statistical parameters but instead using the whole sample as the sufficient statistic is a great idea, as Rafe said.
- The only real danger in looking at data is if you use that to remove parameters from a model. Then the variances are too small. If you fit a model with at least as many parameters as the effective number of degrees of freedom you had in your head when looking at graphs, inferences remain intact. If on the other hand you use a graph to determine that linearity holds, inferences using only one regression d.f. will be anti-conservative.
- I have taken to heart Rafe's "look at the data" edict and have been hearing his words on several recent consulting projects where pharmaceutical companies display longitudinal patient data using PROC SUMMARY in SAS and don't get close to the raw data. Soon I hope to present a new method for choosing and plotting representative curves from a collection of subjects with a repeatedly measured response variable.
- My comment related to the few times in which Pearson's linear correlation coefficient is appropriate for quantifying strength of relationships was related to my default use of Spearman's
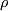 , Kendall's
, Kendall's  , or Somers'
, or Somers' 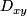 which only assume monotonicity and are not overly influenced by high leverage points.
which only assume monotonicity and are not overly influenced by high leverage points.
ChuanZhou's musings
- I have an impression that some people have misinterpreted Frank's "don't look at data" viewpoint. What Frank meant was clearly put in his second comment above. In fact, I can't emphasize more how important it is "to look at the data". Exploratory data analysis (EDA) is and should always be an essential part of data analysis.
- My understanding of Rafe's point of looking at the data is that we shouldn't look at the data only at their face values, instead we should look at the underlying mechanisms that generate the data as they are.
- With the amount of data points and information increasing dramatically these days, realistically I don't think we can look at each single data point for every project, although I agree we should get close to them. At certain point, we have to resort to the principles of exchangeability, sufficiency and invariance. "Looking at the data" will allow us to check these assumptions, but they will not be enough for us to make valid inference.
- What is inference? The word actually means "generalization". In other words, the goal of doing data analysis is to extract knowledge from the information and generalize it to the general population. Focusing on single data point won't get us there. A balance has to be made.
RobertGreevy's ponderings
- So here is a question following up on Frank's point 2 and Chuan's point 1: what's the impact of changing your analysis method based on looking at the data? For example, consider again the picture that Bryan didn't make. Suppose we had (ignoring Frank's point 4) prespecified an ordinary least squares linear regression of Y on X for our roughly 20 points. We then plot the data, see a highly influential point and say "oops, we didn't plan for that, let's use a robust regression method like M-estimation instead". We haven't changed the parameters of the model, only the analysis method. What's the impact?
- Elaborating on Chuan's point #2, what's the importance of understanding the underlying mechanisms of variation, especially when often this takes the form of a qualitative analysis? As statisticians, our job is the quantitative side of the analysis. Let the subject matter experts make up the theories, we deal with hard data. ... Surely we need to work closely with the experts to understand the sources of variation, but doing our job of quantitative analyses requires making lots of judgment calls, choices that require a good understanding the sources of variation. Consider again the graph Bryan didn't make. My first reaction was I'll just use a robust regression, the regression line will be nearly horizontal. Story over. But suppose I went and talked to the tech who did the assays, and they said, "I remember that outlying point. I did that one last. In fact, it took me the first 19 assays to really figure out how to get enough whachamacallit on the thingamawidge. That's probably why there's all those zeros. That outlying point was my best assay." Without understanding the underlying causes of variation, I run the risk of making a completely wrong judgment call in the data analysis.
Comparing Methods
Dave Airey
Colleagues and I were about to compare an established method of counting cells (stereology on sectioned brain) with a newer method (isotropic fractionator). I read a short and easy to grasp review here, and some papers by Bland and Altman, original and more recent. Are there other general reviews that faculty in Biostatistics prefer, or articles where the authors did an exemplary job? FrankHarrell's comment: Upon quick read the article seems to be excellent. See http://biostat.mc.vanderbilt.edu/twiki/pub/Main/ClinStat/obsVar.pdf Analysis of Observer Variability and MeasureChange for related information.Commentary on Summary Statistics
Rafe Donahue offers up "When Summary Statistics Aren't Enough" --- a short essay with pictures on the value of examining the atomic-level data.Some Important Points about Contingency Table Tests from Campbell, Stat in Med 26:3661-3675; 2007
For those of us who have long disliked Fisher's "exact" test and Yates' continuity correction which tries to mimic it, there is new ammunition and a lot of useful recommendations in this paper. Here are many of the paper's points as summarized by Frank- Latest edition of Armitage's book recommends that continuity adjustments never be used for contingency table chi-square tests
- Discusses E. Pearson modification of Pearson chi-square test, differing from the original by a factor of (N-1)/N
- Cochran noted that the number 5 in "expected frequency less than 5" was arbitrary
- Findings of published studies may be summarized as follows, for comparative trials (quote from Campbell):
- Yate's chi-squared test has type I error rates less than the nominal, often less than half the nominal.
- The Fisher-Irwin test has type I error rates less than the nominal.
- K Pearson's version of the chi-squared test has type I error rates closer to the nominal than Yate's chi-squared test and the Fisher-Irwin test, but in some situations gives type I errors appreciably larger than the nominal value.
- The 'N-1' chi-squared test, behaves like K. Pearson's 'N' version, but the tendency for higher than nominal values is reduced.
- The two-sided Fisher-Irwin test using Irwin's rule is less conservative than the method doubling the one-sided probability.
- The mid-P Fisher-Irwin test by doubling the one-sided probability performs better than standard versions of the Fisher-Irwin test, and the mid-P method by Irwin's rule performs better still in having actual type I errors closer to nominal levels.
- Strong support for the 'N-1' test provided expected frequencies exceed 1
- Flaw in Fisher test which was based on Fisher's premise that marginal totals carry no useful information;demonstration of their useful information in very small sample sizes.
- Yates' continuity adjustment of N/2 is a large over correction and is inappropriate.
- Counter arguments exist to the use of randomization tests in randomized trials.
- Overall recommendation:
- Use the 'N-1' chi-square test when all expected frequencies are at least 1.
- Otherwise use the Fisher-Irwin test using Irwin's rule for two-sided tests, taking tables from either tail as likely, or less, as that observed
Edit | Attach | Print version | History: r14 < r13 < r12 < r11 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r14 - 12 Apr 2010, RobertGreevy
 Copyright &© 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright &© 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Vanderbilt Biostatistics Wiki? Send feedback