Recommendations, Analyses, and Data for Biostatistics Basic and Animal Research Clinic

Archive

Current Notes

22 Nov 2013

Alexia Melo, Eischen Laboratory

• My data involves 4 potential outcomes where I have mice that will get tumors with genes A and B either mutated or not. 1: Wild type A with Wild type B 2: Wild type A with mutant B 3: Mutant A with Wild type B 4: Mutant A with mutant B I want to know if scenario 4 occurs significantly more than the other 3 options. I think I need to use a fisher's exact test, but I need help determining if that is correct. An additional aspect I want to assess is within the Mutant A population (scenarios 3 and 4), does mutant B occur significantly more than Wild type B. I do not know which test to use for this question though.
• Tumors were induced in 50 mice of the same genetic background. Protein A and B were examined in the tumors. Want to see if B mutation rate is dependent on the mutation status of A. Association test between A and B (Fisher's exact test). The direction of effect can be directly described.

27 Sep 2013

Julie S. Pendergast, Division of Diabetes, Endocrinology, and Metabolism

30 August 2013

• Staff: Bryan Shepherd

Bryce Burton, Division of Animal Care

• Interested in doing an experiment to test whether animal cages can be cleaned ever 3 weeks instead of every 2 weeks. This will be measured a variety of ways, but the primary approach is measuring levels of ammonia in the cage. Her design is to measure ammonia levels every week for 3 weeks in several different cages and wants to know how many cages are needed. Several secondary analyses will also be performed.
• We discussed the basic information needed for such a sample size calculation. We based this on the outcome being change in ammonia level from week 2 to week 3 (a sort of paired t-test approach). She appears to want to prove non-inferiority so we discussed the need to select a clinically meaningful level and to design confidence intervals so that they'll be narrow enough to exclude this level. We also discussed the need for an estimate of the variance of the change in order to compute sample sizes.
• Bryce will go to her colleagues, discuss, and look through the literature for some preliminary data. She'll return to clinic at a later date once she's gathered this information and at that point we will finish the power calculation.
• At the end she also mentioned a sub-experiment correlating a measurement in mice with ammonia levels. Mice have to be sacrificed to make this measurement. We deferred further discussion of sample size for this sub-study to a later date.

Dale Edgerton, Molecular Physiology and Biophysics

• Diabetes experiment
• Trying to see if slopes differ between 3 groups. We used his software (StatPad?) and did the analysis. This required a little bit of minor data manipulation and hard coding dummy variables.
• Dale left as a happy client, although his p-value was 0.07.
• Dale may return to discuss additional issues regarding ratios and transformations.

23 August 2013

Carl Moons, Round table discussion of medical diagnostic research

• Please Do Not Schedule Additional Investigators

19 July 2013

Wenfu Lu and Zhenbang Chen, Dept. of Biochemistry and Cancer Biology, MMC

• Targeting histone H3 methylation pathways in CRPC.
• Need to address some issues from a VICTR review
• Specified that an assumption-heavy parametric test (t-test) would be used for n=3. Will increase the sample size to 5 in each group
• Need to look at yield of n=3, e.g., expected width of primary confidence interval, to see if sample size is adequate. Will add sample size justification in the proposal.

Rich Breyer, Division of Nephrology and Hypertension

• The study that we did was in mice. We have two genotypes, knockout and wt, each on two diets high fat and control. Four groups total. These mice develop insulin resistance which can be assessed by an insulin tolerance test (ITT). At time zero, animals are injected with a dose of insulin. Blood is drawn at time points over the next two hours and the response to insulin is measured by assessing blood glucose. N = 3 to 6 animals per group. I am interested in knowing whether the genotype changed the ITT response.
• Can be analyzed on original scale or log scale, not % of baseline.
• Could try generalized least squares for serial data; baseline measurement, time point, genotype, diet type and interaction between genotype and diet could be included as covariates.

05 July 2013

• Staff: Hui Nian, Svetlana Eden
• Client: Opal Lin-Tsai
• Hypothesis: FOXA1(primary outcome), and CK14, CK10, AR (secondary outcomes) is associated with survival.
• Performed analyses: KM curve, Unadjusted and adjusted (including stage) Cox regression. As a secondary analysis, the investigator wanted to look at association b/w FOX1 and CK14 adjusted for stage of tumor. We recommended Cochran Mantel‐Haenszel test.

28June2013

• Consultant(s): Dan Ayers
• Client: None

21June2013

• Staff: Svetlana Eden
• Client: None

14June2013

• Client: None

31Mayt2013

• Client: Marcia Schilling, PMI (pathology, microbiology, immunology)
  • about 20 recipient mice, one group wild type and another group knock-out.
  • Perform ChIP assay in TH2 cells
  • Interested in ratio of AcH3K9 over 3MeH3K27 between control and treatment mice, but do not have data from the same mice
  • K9 and K27 are already quantified as the level relative to house-keeping gene, and could possibly be directly compared between mice.
  • Could use ANOVA. Compare the difference of K9-K27 difference in control and treatment mice, instead of ratio
  • Could use linear regression in order to take into account repeated measures (some mice have both K9 and K27 data)
• Client:SungHoon, PMI (pathology, microbiology, immunology)
  • Reviewer's question: multiple testing
  • But only two comparisons were made in the manuscript. We don't think formal adjustment of multiple testing is necessary. Just need to make clear only two tests are done.

24May2013

• Statisticians in attendance: Dan Ayers, Chris Fonnesbeck
  • Client: Jacqueline Brown, Psychiatry - WT (n=11) and Transgenic (n=12) mice. .Mean time WT spent freezing. Wants to compare slopes. x=frequency of stimulus, 1,..., 12. y=freezing time. time response curves not necessary linear. Every mouse has 12 observations. Mixed models analysis of covariance. Works in the Kennedy center. Recommended she contact Kennedy Ctr statisticians for support.
  • Bryan Fioret , Joey Barnett, Pharmacology - Mouse mode TGFB3. WT(n=) and heterozygous (knockout) (n=). Characterize differences in response to MI Sx between baseline and after treatment. Mixed models analysis of covariance. Fractional shortening (measure of cardiac output) is primary endpoint. Mixed models analysis of covariance (control for baseline output) for repeated measures. Eliminate selection bias by randomly selecting the animals to be sacked at intermediate time points. Recommend contacting Chang Yu, biostatistics faculty member for Pharmacology collaboration plan.

17Mayt2013

• Kirk Kleinfeld, Neurology
  • Patients come to the EMU with seizure and the doctor is trying to decide who is epileptic.
  • Sample size: about 120, and there about 1/3 of epileptic patients.
  • Suggested logistic regression. Outcome: epileptic (yes/no). This association can be adjusted for age, sex, other important patient characteristics.
  • Number of variables included in the model is defined by the minimum between outcome = 0 and outcome = 1. If you have 120 patients and 40 epileptic, we can include maximum 40/10=4 variables. He will discuss with advisor which variables to put in the model.
  • Need to attend another clinic to meet a VICTR biostatistician to get an estimate of how many hours the work takes.
• Sarah Njoroge, pathology
  • There are wild type of mice and mice with a cystic fibrosis gene knocked out, and other groups, overall 6 groups, with 6-7 mice in each group. The researcher is blinded to what mouse belongs to what group. They have a score of how much blockage they have in intestinal villii. The higher the score is the worse is the blockage.
  • Hypothesis: Those with knocked out gene have more severe blockage.
  • issues: difference between groups can be cause by difference in time when blockage was measured.
  • Suggested analysis: for two comparisons of interest use Wilcoxon Rank Sum test: KO vs KODHA p-value is 0.0178, KO vs KOAF p-value is 1, and the p-value is 1 for all wild type comparisons.
  • Suggested to show all data in a strip chart per each group.

10Mayt2013

• Mesh is placed under vaginal epithelium to prevent repair (?) from failure. Patients complain about pain and ask to take it out. The question is whether the pain is better after the surgery. The investigators collected data: smoking, diabetes, chronic pain, other data. Surgical data (what site mesh has eroded). The pain is recorded in three categories: worse, no change, better.
• 231 patient: 169 (improved), 21 (worse), 14 (unchanged)
• First, we suggest descriptive summary: correlation of pain with collected data (see above), and two-by-three tables (smoking by pain level, for example)
• Options: get help through a collaboration plan, or apply for VICTR, or come to the clinic several times
• The analysis suggested here:

24Apr2013

• Statisticians in attendance: Dan Ayers
• Bernado Maynou, Peds Infesctious Diseases, Post-Doc.Does a panel of drugs reduce viral protein synthesis. Vehicle Control for an entire panel. 3 drugs with 3 concentrations for each drug. ANOVA with Dunnets's to compare control vs each drug.
• Lewis Kraft, Chemical and Physical Biology, Grad Student. Wanted to check and see if AIC could be used to compare models; model 1 is two groups come from diffierent distributions and model 2 is they come from the same distribution. Objecting to conservatism of bonferonni adjusted tests. Discussed Holm test, likelihood ratio and Bayesian approaches.

12Apr2013

• Statisticians in attendance: Frank, Chun, Qi, Jacob, Yaoyi, Liping, Val
• Louis Kraft (CPB) came to discuss a scenario where there are 4 subjects, each measured 4 times on a variable. Can we do some test on whether the 4 subjects differ?

15Mar2013

John Williams

* Statisticians in attendance: Bryan, Dave, Val, Minchun, Xue, Yuwei, Yaoyi * We did an analysis for him of his mice data. We compared entire trajectories by fitting a quadratic model by time for each group, and testing an interaction between group and trajectory. We also did an analysis at the peak time, highlighting that this analysis isn't exactly right because we saw the data first to determine the peak. It's OK to include, however, if one mentions in the write-up that this is what was done. Bryan saved the code and will send them the analysis results.

08Mar2013

Jamie Reed

• Resonse field territories of digit representations in area 3b following spinal cord injury
• The objective is to quantify cortical reorganization within the hand representation of primary somatosensory cortex in monkeys after they show behavioral recovery a spinal cord lesion.
• Four control monkeys and four injured monkeys
• 10*10 electrode array. target region 2mm*2mm
• outcome: number of neutrons that responded

15Feb2013

Consultants: Chris Fonnesbeck, Dan Ayers

Client: Quan Mai. Model building for a ordinal scaled (3 groups) outcome with >9 predictors. 50 observations, 37 outcomes. Groups of parameters by content knowledge. 3 categories. Use data reduction, AIC for groups of variables. Propensity scores as variable surrogates and examining correlations of variables within groups for potential exclusion.

Client: Patrick Page-McCaw, Dept. Physiology. Physiologic genetics. Test 26000 genes to see if they affect phenotypes.

01Feb2013

Consultants: Chris Fonnesbeck, Dan Ayers

Client: Yin Guo

Preliminary data available for control and treated mice. Which estimates of variance do I use in PS for sample size calculation. Where can I get estimates of variability for the treated group where we have no actual data?

Client: Ernest Yufenyuy

Which test do I use for 15 pairwise comparisons using the same control group. Answer: Dunnett's pairwise t-tests to control the experiment-wise type I error rate.

25Jan2013

Consultants: Leena Choi, Ben Saville

Meg McKane, Peds cardiology fellow

• MSCI application with Robert Sidonio and Michael DeBaun
• Estimate prevalence of asymptomatic thrombosis in infants with single ventricle complex congenital heart disease
• Focus on patients after the first stage of surgery (Shunt)
• Determine whether asymptomatic thrombosis is predictive of worse outcomes (death, LOS, etc.)
• Need to adjust analysis for relevant confounders. May need to consider propensity scores depending on outcome

Ghazal Hariri, Chemistry

• Needs power calculation for mice study of drug effect on tumor size
• 13 Control groups and 5 experimental groups
• Has preliminary data on controls and a treatment group that could be used for power calculation
• Mice are injected with tumors, monitor the change in tumor for 2 weeks.
• Mice are sacrificed when the tumors reach 1cm in size. Controls reach the size quickly. Treatment groups may not reach that size during study duration.
• Possible outcomes:
  • Time to 1cm in size. Problems: treatment group may not reach 1cm. Measurements may not occur every day.
  • Calculate individual slopes and compare the distributions of slopes between groups
  • Compare change in tumor. Problems: Animals are sacrificed when they reach a certain size
• Recommendation: Decide on an outcome, send the preliminary data to biostat clinic and come back another day

18Jan2013

Consultants: Bryan Shepherd, Frank Harrell

Yin Guo, Pathology, Microbiology, and Immunology graduate student

• Sample size, 4-group problem
  • Is one of the pairwise comparisons of dominating importance?
  • Could power to detect the hardest-to-detect comparison
  • ANOVA F-test power
• But the design is really a 2x2 factorial
  • Interaction test will have the lowest power of all the tests that could be run
  • Size the study to not miss the interaction effect
  • Easiest thing to calculate is the precision (margin of error) of estimating the interaction effect. In large samples this is 1.96*s*sqrt(4/(n/4)) = 1.96*s*4/sqrt(n); solve for n
  • If acceptable margin of error in estimating this double difference is M, solving for n gives n = [1.96 x 4 x s / M]^2 at the 0.95 confidence level
  • Margin of error is 1/2 the width of the 0.95 confidence interval
  • Note that an interaction effect (double difference) has a variance that is 4 times the variance of a single difference

21Dec2012

Consultants: Dan Ayers, Frank Harrell

• High-level language for Clin Trial Development?

30Nov12

Kyra Richter and Thyneice Taylor, Pathology, Microbiology, and Immunology

Consultants: Leena Choi, Frank Harrell, Bob Johnson

• TNF-a, IL-10, IL-2, etc. in healthy controls (n=20) vs. sarc. patients (n=31)
• Discussed a joint "profile" analysis using logistic regression to relate all variables to probability of sarc.
• Good project for VICTR funding. To cover biostatistics assistance for manuscript all the way through to a grant application may require 50 hours ($5000) - get $2000 and home dept. pays 1/2 of remaining $3000

02Nov12

Jeremy S. Pollock, PGY-2, Department of Internal Medicine

• Apply for VICTR to get statistical help for re-analyzing registry data with a binary outcome and many potential confounding variables. Suggested using propensity score to adjust for potential confounding variables in a logistic regression analysis. Estimated 35 hours of work, a total of $3500.

26Oct12

CJ Stimson, GU Surgery

• Regional analyses

Sheldon Holder, Hematology & Ontology

• Power and sample size

28Sep12

Vickie Keck MS VMD, Veterinary Resident, Division of Animal Care

• Zebrafish study

John Virostko, Instructor, VUIIS

I have a timecourse of imaging results for mice that become diabetic over the course of the study and those that did not become diabetic. I would like to determine whether there is a statistical difference in these two cohorts. I've attached the weekly imaging results for these two cohorts in the '.csv' file. I have also performed a binary logistic regression analysis with the aid of a colleague and wanted to make sure I am presenting this data correctly ('.doc' filed attached). Note : files are in ~/clinic/basicSci

21Sep12

Statisticians: Val, Bryan, Dave Airey

Dikshya Bastakoty and Desirae Deskins

We recommended using intraclass correlation. Here is some R code with their data:

x<-c(117855,105400,83425,82540,74250,48300,85020,81620,53580,41810,95700,98900,95760,78880,89100,76650,51600,45360,164320,152250)x1<-c(117855,83425,74250,85020,53580,95700,95760,89100,51600,164320)x2<-c(105400,82540,48300,81620,41810,98900,78880,76650,45360,152250)x<-cbind(x1,x2)
donor<-c(1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10)
est<-icc(x,"oneway")

est

# uses the irr package

### Here is the output

 Single Score Intraclass Correlation

   Model: oneway 
   Type : consistency 

   Subjects = 10 
     Raters = 2 
     ICC(1) = 0.927

 F-Test, H0: r0 = 0 ; H1: r0 > 0 
    F(9,10) = 26.2 , p = 8.41e-06 

 95%-Confidence Interval for ICC Population Values:
  0.748 < ICC < 0.981

24Aug12

Consultant(s): Dan Ayers, Robert Greevy, Bob Johnson, Dandan Liu, Chun Li, Frank Harrell

Client: Vaibhav, Dept. of Physics

• Additive noise model or multiplicative noise model for estimating distribution of pixel intensity (signal/noise) in ROI's among 5 images.

27Jul12

Consultant: Dan Ayers

Client: Yasin Kokoye, Assistant Professor, Pathology (Comparative Medicine),Clinical Veterinarian, Division of Animal Care

• Two projects
  • Prevalence of Helicobacter species in mice received from non-commercial sources and entering institutional quarantine.
  • Murine Norovirus (MNV) affects Complete Blood Count (CBC) values of CD-1 mice.
  • Data available and consult given. Analysis beyond the scope of Clinic so suggested contact with BCC.

13Jul12

Consultant: Dan Ayers

No Clients

06Jul12

Consultant: Frank Harrell

Client: Katie Ryan, Chin Chiang CDB

• Size of cerebellum
• 30 slices per animal, may use 10
• Compare control & test groups
• Sets from different litters; ages may vary across sets
• Example model: Y= log(cell count / area) [need to check residual plots to see if should have taken log]
• Y = overall intercept + litter effect + intervention effect + individual mouse weight effect (covariate; probably not needed for per unit area analyses)
• Correlation structure: no correlation within litter once account for litter effect; correlation between any two slices from the same mouse: AR(1) serial correlation structure [autoregressive moving average; exponential decline in correlation as you move farther apart]
• Generalized least squares: generalization of multiple regression to add correlation structure (slices)
• Y = beta0 + beta1*litter2 + beta2*litter3 + beta3*experimental
• Alternative: summary statistic approach: one number per mouse, n = # mice, no way to take litter effect into account
• For GLS need data to be in specific form
• Can use an equal-correlation pattern if slice sequence numbers are unknown

01Jun2012

Dan Ayers Consulting

Melissa Fischer, Post-Doctoral Fellow, Department of Pathology

• Allogenic BMT in mice. Transplant mutant null into wildtype (wt).
• Exp 1. Control is wt cells into wt mice. Treatment is mutant null cells into wt mice. Transplant sequentially every 16 weeks until a mouse in that line dies (is unable to reconstitute). Binomial (Dichotomous) sample size estimate of 19 per group for p0=0.5 and p1=0.1 with 5% Type I E and 80% power. Melissa will train herself on PS.
• Exp 2 Competitive BMT Mix 50% CD45.2 wt and CD45.1 wt cells into wt mice (which are CD45.1). Treated group is 50% CD45.2 mutant null cells + 50% CD45.1 wt cells into CD45.1 wt mice. Transplant sequentially, but measuring percent reconstitution of CD45.2 every 4 weeks. If no CD45.2 changes to 40%/60% in 16 weeks, transplant second mouse in the series.

27May2012

Dan Ayers Consulting

Dayanidhi Raman, Department of Cancer Biology

• Stat consult for VICTR grant. N=71 human tissue microarray. Score (pos/neg) presence in nucleus of LASP-1. Hypothesis: greater incidence with higher clinical grade. Chi-square test. Effect size detected in 71 patients vs 36 patients in other categories.

Pampee Young, Department of Pathology

• Response to reviewers comments.

27Apr2012

Dan Ayers Consulting

Ron Emeson, Department of Pharmacology

• Analysis of Mendelian genetics - have a distribution from a heterozygous cross that should be in a 1:2:1 ratio. How many pups are needed to detect deviance from this ratio. What power do I have for 100 or 120 pups.
• Estimate effect size from preliminary data and estimate number of animals necessary to have 90% probability of detecting that effects size with a type I error rate of 5%.
• Tables of samples sizes required to detect (p<0.05) observed effect sizes and table for effect sizes detectable with 80% and 90% power for 75, 100, and 120 pups were provided.

16Mar12

Patty Chen, Pathology Microbiology Immunology

• Question about how many animals to sample
• 3/n rule: set the maximum acceptable probability of disease; set to 3/n and solve for n
• Need true cost-benefit analysis to get a definitive answer

Paul Yoder and Kristen Bottema-Beutel, Peabody Special Education

• Kids < 24m with autism
• Randomized to experimental vs. control
• Examining types of dependent variables (DVs)
  • Some directly affected by treatment, some indirectly affected
  • 4 DVs in each of 2 classes of DVs
• Is a type of meta-analysis
• Studies have similar treatments but different DVs
• Some of the studies may be willing to provide raw data
• Issues about standardized effect sizes using pre-treatment score covariate adjusted means
• Potential for a stratified rank method; assumes that raw data are available from all studies; easy to visualize using one DV; DV is ranked separately for each study and we assume that low-to-high rankings are equally meaningful across studies; not assumption about metrics other than ordering assumption
  • Best worked-out method in the literature is the stratified Cox proportional hazards model
  • Could do a stratified Wilcoxon test or stratified proportional odds model (generalization of Wilcoxon-Kruskal-Wallis)
• Can compute average ranks across DVs; this has been worked out for the case where there is only one stratum and no covariate adjustment ( Peter O'Brien paper)
• The bootstrap can be used to get confidence limits on a global summary of treatment effect

24Feb2012

Consultant: Dan Ayers

Client: Kristin Poole, Ph.D. student, Biomedical Engineering

• Mouse experiment with primary objective to test the effect of surgical induced ischemia on HgB saturation and pO2. Each moouse was surgically treated to induce ischemia on the right limb and Hgb and pO2 measured on both the right and left limbs at day 0, 3, 7, 14, and 21.
• Plotted HgB and pO2 profiles over time by treatment, showed a set of summary statistics and conducted LMM for each variable.

Client: Dina Stroud, Ph.D., Thomas Atack, Dept Medicine.

• 2 sets of data. Small sets of data.Q R^2 PCR accross tissuetype and genotypes, BioRad. Talk about deltadeltaCt, efficiency and adjusting for efficiencies. Come back with data.
• Use the Wilcoxon ranks sums test to compare measurements across independent groups.

02Dec2011

Consultant: Leena Choi

Client: Sarika Saraswahi, Pathology

• Revisit of data analysis of testing of difference of two treatment( 6 mice, each received two different treatments)
• Performed paired t-test before, suggested by reviewer to do log transformation, our suggestion is to do non-parametric Wilcoxon signed rank test, and present data in raw values

26Aug2011

Consultant: Dan Ayers

Client: Mike Corey, Surgery

• Review of REDCAP data base.
• Suggestions made for keeping data continuous if possible, enter dates, not time intervals, test database.
• Apply to VICTR for statistical support.

Client: Rimal Hanif, Senior Med Student

• Survival Dataset- 50 patients, 2 censored for death.
• Suggestions made for keeping data continuous if possible, enter dates, not time intervals, test database.
• Patients with missing survival time were excluded and then KM plot was made
• Apply to VICTR for statistical support.

05Aug2011

Consultant: Leena Choi, Frank Harrell, Dan Ayers

Client: James Crowe, Vaccine Center

• Data A: Compare treatment vs. control for survival time
• Need to make an appropriate data set for survival analysis from aggregated percent data per group
• 6 mice per group: may not provide enough power
• Use dose (0 for control, 2, 20, 200) dose as a covariate in Cox proportional hazards model
• Data B: lung titers
• Use a pooled regression model

22Jul2011

Consultant: Dan Ayers

Client: Julie Pendergast, Post-doctoral Fellow, Dept. of Biological Sciences

• Need sample size estimates and instruction using Sample size software for 2-group design. Prior data for control (n=4) (vehicle) and treatment (leptin) (n=5 )treated animals. Outcomes include caloric intake, phospho-stat3 and total stat3.
• Data provided in EXCEL spreadsheet. Means, s.d.'s and t-tests calculated by Dan A. in spreadsheet itself.
• Discussion of endpoints, role of total stat3 as a control variable and whether or not to use the ratio of phospho-stat3/total stat3 or ANCOVA.

Client: Raafia Muhammad, Research Fellow,Cardiology

• Seen on Wednesday clinic
• Comparing family history (yes,no) in a model to include burden score, and response taken at 0, 3, 6, and 12 months. Large amount of missing data.
• Hyp-1 Familial patients require more ablation therapies than non-familial patients (potentially modified by the number of therapies and burden). Longitudinal score of burden score. Start clock at informed consent and model time to ablation using Cox regression, with famiial indicator, therapy time line and burden score. Little indication of a an absorbance competing risk.

24Jun2011

Consultant: Dan Ayers, Chris Fonnesbeck, Leena Choi

Client: General Discussion

06May2011

Consultant: Dan Ayers

Client: None

06May11

Consultants: Dan Ayers, Chris Fonnesbeck, Pingsheng Wu

Client: Pingsheng Wu

• Study Design: Effect of long acting Beta agonist on asthma management and control. Two large RCT's that replaced long term beta agonist with placebo. Show increased risk of AE's including sudden death, emergency room admissions, etc. Another study shows no increased risk with addition of shortterm corticosteroids. Meta analysis concludes LT B-agonist + coricosteroids eliminates the risk. However, low power.
• 10% to 14% asthmatics among PEAL network (TennCare and 4 other HMO's) + DOD data. ~ 10 million unique records. 1998 to 2009
• Problem: longitudinal but people go in and out of the system (missingness)
• 4 regimens standard
• SA1 - Describe treatment compliance
• SA2 - Compare benefit/risk of 4 regimens for intubation, ED, mech vent, death. Time to event or number of events as endpoint
• Consider time dependent covariates in time-to-event, multi-state model.
• Consult further with Chris Fonnesbeck and/or Bryan Shepherd.

Client: Dan Ayers

* Problem: Simulate data for a proportional odds model and cumulative logit. * Generate normal errors, add linear model, transform to logit scale.

29Apr11

Consultants: Dan Ayers, Chun Li, Heidi Chen, Frank Harrell

Kate Gurba, Neurology

• 5 time points
• Issue of relative vs. absolute change (measurement is integrated intensity using Image-J)
  • To demonstrate the adequacy of a ratio scale make a Bland-Altman plot (y=difference in logs, x=average or sum of logs); should have flat central tendency and constant variability going horizontally; to check adequacy of ratio (without taking log) plot ratio vs. geometric mean
• General hypothesis is whether the time-response profiles differ between groups
  • If linear, this amounts to looking a changes in slopes or in slopes and intercepts
  • If quadratic, have a linear and a square component
  • Mean curves appear quadratic
  • For a given day, normalized to maximum (last measurement) gamma intensity at 20m; assumes this is measured without biologic variability or technical error
  • Unified approach would be preferred: allow for a "day" effect that is a random effect if a regression model

April 08, 2011

Topic - sample size justification (K99 proposal)

• Diana Sarho Hearing and speech
• Dependent variable: Neuron response, Integrative activity?
• Sequential treatment, possible carryover effects
• Between-region comparison within the animal; 2 animals.

March 25, 2011 - Dan Ayers, Chris Fonnesbeck, Dan Byrne

Topic

• Outcomes research

March 11, 2011

Bin Li, Pathology

March 3, 2011 - Dan Ayers, Chris Fonnesbeck, Sam Nwosu, Yuwei Zhu, Alex Zhao, Yaping Shi, attending.

Peggy Kendrick, M.D. - Allergy, Pulmonary Medicine, CCM

• Animal Studies. Time to diabetic event. Censoring and animals die before observed event. Explain logrank test and (generally) how the Chi-square statistic and Wilcoxon rank sum statistic is calculated. Discussed reasoning for selection of parametric and non-parametric tests. Show R function for competing risk analysis. Discussed reasons for competing risk vs standard Kaplan-Meier.

Feb 11, 2011

Beth Drzewiecki, MD - Clinical Fellow, Division of Pediatric Urology (RT-PCR data analysis)

Jan 28, 2011 - Dan Ayers attending

Olivia Giddings, MD and Lisa Lancaster, MD - Instructor, Department of Pathology

• Vague VICTR request suggesting consult with clinic
• Presented a Kaplan-Meier Curve comparing survival of 2 groups of patients, compliant and non-compliant with time zero at time of diagnosis.
• Problem identified was guarantee time for compliant patients.
• Recommended time-dependent covariate analysis.

Samir Aleryani, P.h.D - Instructor, Department of Pathology

• Vague VICTR request to get sample size advice from Friday Clinic
• Unable to use PS in clinic because GUI did not translate well.
• Preliminary data requested and received Jan. 31, 2011.
• Example sample size estimates planned.

Jan 14, 2011

Kendall, MED

• P-value for log-rank test
• library(survival)
  
  d <- read.csv('Documents/Documents.csv', header=TRUE, as.is=T)
  S <- Surv( d$TIME, d$EVENT)
  ?Surv # get documentation with a ?
  km <- survfit( S ~ GENOTYPE, data=d )
  km # will give you median survival with confidence interval
  km2 <- survdiff( S ~ GENOTYPE, data=d )
  ?survdiff #
  summary(km)
  plot(km, las=1, main='main', xlab='xlab', ylab='ylab', col=1:2 )

29 Oct 10

Joe Hall, ENT

• Would like to compare wound healing using 4 different blades. Outcomes are short term swelling and long term tensile strengths of the wound. These are measured at 0, 21, 28, 35 and 42 weeks. Each pig has 20 total incisions at each time and with each of the 4 blades. The primary endpoint are differences at 42 days.
• He needs a sample size an analysis plan for an internal application and for IACUC. He will email Jeffrey about the BCC, and think about what detectable alternative is acceptable.

25 Oct 10

Lee Shama, ENT

• Does nasal washing effect the SNOT survey total score? 31 patients all participated in nasal washing and were followed at specific time points. (More patients were enrolled, but only 31 had follow-up visits). The survey has 20 questions from 0 to 5 for a total of 100 points; 0 is the healthiest.
• Percent change is not appropriate. However, testing to see if the slopes are 0 is ok.
• Recommend trying VICTR for some statistical support.

David Airey

• Investigating how many eggs nematodes lay after a set period of time. Each worm starts with a certain number of eggs "on board". The hope is the timing is such that worms have not laid all their eggs before being assayed. The max number of eggs to lay is roughly 20. The total number of eggs a worm started with can be ascertained at the end of the study. The rate of interest is not proportion of eggs dropped, but the number of eggs dropped before time t.
• David had questions about using Poisson regression and negative binomial regression.

17 Sept 10

Brad Creamer, Biochemistry

• Would like to cluster groups of cell lines based on IC50 counts. It is not clear how to cluster on one variable, so referred to Yu Shyr who has done this before.

10 Sept 10

David Airey -- Pharmacology

• Amino acids (20) measured in various strains of mice (50)
• Set of recombinant inbred mice
• Looking for genes that can control metabolic pathways
• Amino acids appear to be correlated, based on PCA
• Trying to do confirmatory factor analysis
• Two factors already known; looking for amino acids associated with factors
• ~15 aa appear to be associated with first factor
• May be too many aa's associated with first factor to ascribe meaning to that factor
• Referred him to Irene Feurer's seminar next week

13Aug10

Ehab Kasasbeh, Cardiovascular Medicine

• 13 dogs, intracoronary injection of vasoactive drug, looking at blood flow in coronary (peak velocity)
• Drug: par; expect decrease in coronary blood flow
• Differential effect in response to injection due to age of dog: < 12 months vs > 12 months
• A=1, B=2 in data: A=< 12m, presumed healthy, AL, B=unknown age, presumed > 12m, medical history not known in detail, NY
• Response to acetylcholine; analysis based on health of endothelium
• Different animals studied different durations; caused by hypotension or ventricular arrhythmia etc.
• Inaccurate readings censored, e.g. instant change to zero flow; fairly certain these were artifacts
• Each animal had it's own shift or intercept
• Not obvious that division is the proper normalization
• Normalization is generally inappropriate vs. using a model that allows each dog to be shifted from the other dogs
• Very first step = spaghetti plot
• If need to look at raw data in a future clinic: need these columns: dog ID, dose, time, flow; one row per dog per time

Saras Viswanathan, Molecular Physiology and Biophysics

• 4 experimental groups with LDL knockout mice; olive oil vs fish oil in presence of indomethacin
• Expect reduction in plasma lipids in mice given fish oil
• 2x2 factorial (4 cages); 15 mice per cage; age matched; assignments to cages thought to be random but not guaranteed to be so
• Hypothesized that in the presence of indomethacin, a synergistic effect with fish oil
• Another drug NS was used; this was actually a 3x2 factorial design; NS temporarily omitted because the results for it were not as impressive
• Suggestion: Fit 2x3 factorial using 2-way ANOVA; make all contrasts of interest based on the single unified model
  • This model will have a single variance term and will allow for interactions
  • Also allows formal test of synergism; total interaction effect has 1x2 d.f. = 2 d.f.; test of whether indo or ns affects the fish oil effect
• Whether overall interaction test is significant or not, specific fish-olive oil contrasts can be made
  • single comparisons (e.g., fish - olive in indo); may need a multiplicity adjustment (more P-values -> more chances for type I error (false positives))
  • simultaneous comparisons (e.g., test fish - olive difference in any of the 3 groups; 3 d.f.)
• Check assumptions: normality of residuals, equal variance of residuals; may lead to a transformation of cholesterol; 6 box plots may be a good choice

6August10

Tom Thomas, Department of Medicine

• Two mice, one with knockout, one without.
• For each mouse, there are six conditions, four dosages for each condition, three experiments for each condition.
• The goal is to compare the curves for the two different types of mice.
• Suggest: calculate the AUC value for each experiment, and compare using Wilcoxon rank sum test.

Genie Moore, Department of MPB

• Question about design for five years grant: can I use historical control, if not what will be the better design and how to justify it.

Jill McDaniel, Department of Special Education

• Two groups to study nose pokes, each group will have 12-15 mice. The goal is to compare the response for each session and the curves of two groups over 10 extinct sessions.
• Suggest: Wilcoxon rank sum test for each session, and proportional odds model to compare the two groups and control for the baseline.

23July10

Alexia Melo - Department of Pathology

*Two Projects

1. 1. The aim to see if there is a difference in radioactivity is solutions that have Pig3 protein and solutions that do not. Wilcoxon rank sum test is advised. Also doing both both arms on the same day and repeating this process over several days. 3 technical reps of each a day are preferred. Plots will be a great way to show the magnitude of the differences and the variability in the process.
   2. We aim to compare immunofluoresence in cells in a culture between 4 groups at 2 time points. 50 cells will be examined in each group/timepoint. One group is a negative control and is ignored for the purposes of statistical analysis. This will leave us with what we call a 2x3 factorial design. Ideally this design is one we would use a "fancy" model to analyze. For your purposes we recommend meeting with a statistician who can show you how to do this. Of the three groups, there is one control, or wild type, group and 2 mutant groups. In the control group we expect approximately 50 foci to be found in each of the 50 cells examined. We discussed how these 50 cells will be selected for the study, including randomization techniques.

16 July 10

Shaoshan Liang and Shuwei Wang - Department of Pathology

• IGA nephropathy; 4 variables - prognostic variables from a previous paper
• Response variables: 15% drop in GFR; time until ESRD development
• Discussed http://www.nature.com/ki/journal/v76/n5/pdf/ki2009243a.pdf(Kidney International 2009)
  • Severe statistical problems including: dichotomization of continuous prognostic factors and use of cutoff on GFR to form an outcome variable, making the meaning of the outcome dependent on where patients start; treated % drop in GFR of 49% same as 1% and 51% same as 100%; used "multivariate" to refer to multivariable models
  • Treated time-dependent covariates as baseline covariates
  • Stated that multivariate models were tested using "standard statistical rules" (appendix) without explanation
  • Stated that predictors needed dichotomization if had a skewed distribution; in one case used a square root transformation without checking its adequacy
  • Removed "outliers" from individual-patient regression line fits (!!!). This is a complete manipulation of the data.

25June10

Alexia Melo and Shidrokh Ardestani - Department of Pathology

PIG3 is melanoma protein for which we want to compare the expression, via percent cells positive between malignant tissue and surrounding normal tissue. So there is a correlation between the "normal" and surrounding "malignant" tissue because they come from the same patient. Estimated percent positive cells is 50% in normal tissue. A differential expression of 20% (lower or higher - 30% or 70%) would be biologically relevant.

1. Type I and Type II Errors - 0.05 and 0.1

2. Measurement scale (% of cells positive for PIG3)

3. Primary endpoint - paired difference in percent of cells positive between malignant and adjacent normal cells.

4. Variability - estimated standard deviation of the differences in percent positive cells.

5. Effect Size - smallest magnitude of difference one would be disappointed in missing (20%).

Added recommendation: Conduct a pilot study!!! This will take much of the guesswork out of sample size calculations inherent in not knowing the variability of the measurements (and the experiment in general).

28May10

Louise Rollins-Smith an Jeremy Microbiology and Immunology

CTSA cannot help because its not human tissue. Come back to clinic, or look into our charge-by-the-hour service. Contact Jeffrey Blume for the charge-by-the-hour service.

• For the second data set, consider using Fisher's LSD. This process looks to see if any comparisons are significant all at once (ie. a single p-value). If this first step is not significant, stop here. For this first step use Kruskal Wallis test. If this is significant, continue with the pair-wise tests of interest with Wilcoxon rank-sum tests.

Thomas Kehl-Fie Microbiology and Immunology

• Has a 2 by 2 factorial design. There are wildtype and mutant mice, infected with either the wildtype or mutant bacteria. The outcome is on the log scale and has a limit of detection problem. In two of the 4 groups at least half the mice are at the low detection limit.
• Strongly recommend not using just the low limit as the value because this can incorrectly reduce the variation in your data and you can end up with a falsely significant p-value. We recommend using a nonparametric test that relies on rank instead of actual value. These won't help with the factorial design as nicely as the next suggestion.
• The proportional odds model can help with finding the "double difference", or the difference bewteen the differences (the interaction term in the model). It also can handle the lower limit of detection problem nicely. The model would look like this...
  • log(bacteria)= mousetype+ bacteriatype+ (mousetype*bacteriatype)
• Set up a column for mouse type, and one for bateria type. Depending on what software you use, these will either need to be numeric (ie. 0 and 1) or characters ("mutant" and "wildtype"). Also include a column for the outcome (or log(outcome)).
• Recommend getting your data in this format in excel or some other easy spreadsheet and sending it to the clinic address and returning so we can help you run this and interpret the results. We can also use your pilot data to help you figure out how many animals you will need for a full study.

Ann Choe and Adam Anderson BME/Radiology

• They have a model with an outcome and two explanatory variables that are correlated and are curious how to deal with analysing/explaining this. There is no scientific reason A and B would be correlated.
• Recommend three models as below...
  • full model outcome=A+B
  • reducedA model outcome=A
  • reducedB model outcome=B
• Next, compare the total sum of squares in the full and reduced models to see the individual contribution of each variable.
• To display the model try a plot with A on the x-axis, B on the y-axis and color the "pixels" based on the estimate of the outcome from the model. For example black could be low estimated outcome and white could be high estimated outcome and greys fall in between. Summarize model fit with root mean squared error perhaps.
• This plot would also work if you added an interaction term to the model.
• Look into an interaction between A and B.
• AIC and BIC can also be used to compare models. Based on the specific software higher or lower AIC or BIC may be better. If they are close, you may choose the simpler model. BIC is "ultra-conservative".
• The Kennedy core can help you with specific model building or graphic creation.

7May10

Tiffany Walker and Robin Broughton - Microbiology & Immunology, MMC

Primary consultants: Leena Choi, Frank Harrell

• Need assistance with VICTR voucher pre-review
• Role of LFA1 (cell surface adhesion molecule) in HIV infection (does it limit replication or spread)
• Primary T-cells isolated from blood; stimulate to promote T-cell expension
• Treat with inhibitor of LFA1; look at resulting cell signaling
• 3 groups: untreated, treated to inhibit adhesion, treated but not to inhibit adhesion
• 3x2 factorial: crossed with HIV+ HIV-
• Response: several assays: apoptosis, viral rep, infection
  • Western blot yes/no; most are gradients, most are direct measurements - e.g., % of cells that are positive
  • Come from flow cytometry
  • Start with a similar volume of cells; assume that denominator of % can be ignored
• Time 1, Time 2 repeated, Time 3 repeated (non-independent replicates to see growth over time)
• 6h post treatment harvest cells run assays; 24h harvest cells from the same frozen pool, do same assays;

Frozen cells
    |  thaw
Culture (PHA-L)
    |  3 days
Treatment (IL-2) -> Tcell growth
    |  day 5-6
Infect (HIV) -> Beginning
    |  24h
Treat (w, w/o mAb) -> 6, 12, 24, 48h -> Assays

• 6 groups x 3 times -> 18 independent measurements
• Initial statistical analysis plan: t-test on differences
• VICTR pre-review comments: normal distribution assumption may not be justified
  • If percents hover between 20%-80% a normal distribution may be adequate
  • With more extreme percents, transformations may yield normality (e.g., arcsine square root)
  • Alternative: non-parametric tests (e.g., Wilcoxon-Mann-Whitney); problem with 3 measurements per group
  • Interested in distributions over time
  • Major comparison is double difference -> interaction between group and HIV status
• Classical 2-way ANOVA; get one best (pooled) standard deviation if ignore time
• Multiplicities: 3 times, 3+ assays; one solution is to priority order hypotheses without looking at the data
• Recommend 9+ separate tests of interaction between group and HIV+-; each is 2-way ANOVA on arcsin square root of proportion of cells exhibiting the characteristics of interest (2 double differences); assuming 6 groups are independent
  • n=18; error degrees of freedom 18-2-1-2 = 13
• How were 3 replicates per group chosen? Need to envision the size of the effect one does not want to miss.
  • This is stated in terms of the biologic effects one does not want to miss, not the effects observed in a previous experiment
• Another possible approach: report confidence intervals and emphasize the root mean squared error (residual standard deviation from the overall ANOVA model)

23Apr10

William Wolfle - Rheumatology, Dept. of Medicine

• qRTPCR Data
• Group 1 - Wildtype (n=6), Group=2 -DTG (n=8)
• Technical Replication: 2 within same day. Repeat qRTPCR completely with same tissue 4 days.
• Groups of mice, e.g. 2 WT , 2DTG may be done over different months (normalizing with plasmid positive control recommended).
• Block on Days. "Randomized Block" ANOVA parametric
• Friedman's Test For NonParametric Test (loss of power).
• OK to average over technical replicates
• Examine REST? software.

16Apr10

Peggy Kendall - Allergy Division, Dept. of Medicine

• B-cells, treated vs. non-treated
• Y= # mutations
• About 6 animals; used multiple mice to get enough volume for samples
• Pooled samples; sample = inflamed pancreas islets
• Don't example samples from same mouse to be more similar to each other than samples from two different mice
• Good options: Poisson or proportional odds two-sample problem; Poisson is sometimes said to be more appropriate when the counts are bounded
• A large P-value would be interpreted as there being insufficient evidence for a difference; one may not conclude that there is no difference
• Best to use confidence limits; for Poisson, this would be in terms of relative risk of a CDR mutation in one treatment group over another, or in terms of the ratio of two means (anti-log of Poisson regression coefficient)

26 February 2010

Dan Ayers, Frank Harrell, Ben, Yu Wei

Yu Wei - pre and post titers. need a confidence interval for the ratio of the pre and post values. Does she take the mean of the pre, post then the ratio?

Frank would take the with person ratios, then calculate the medians of the ratio and bootstrap the CI.

19 February 2010

Maria Maples

• We created some figures for Maria's poster using the following code:

d<-read.csv("excel.csv")

time<-d$time cum.dose<-c(0,0, .00000025, .00000075, .00000175, .00000375, .00001, .00001125, .00002125, .00004125, .00007, .00012, .0002, .0004, .0007, .0012, .0022, .0042, .007, .012, .02, .04, .07, .12, .22, .42, .7,

1. 1. 1. 1. 2,
         2. 2,
         3. 2,
         4. 2,
         5. 2,6.2,8,10,14,19,24,29)

plot(time,cum.dose,xlab="Time (hours)",ylab="Cumulative Dose of Indapamide (mg)",las=1)

pdf("cum-dose.pdf") plot(time,cum.dose,xlab="Time (hours)",ylab="Cumulative Dose of Indapamide (mg)",las=1,col=4,pch=19) lines(time,cum.dose) dev.off()

pdf("cum-dose-log.pdf") plot(time,log10(cum.dose),xlab="Time (hours)",ylab="Cumulative Dose of Indapamide (mg)",las=1,axes=FALSE,col=3,pch=19) lines(time,log10(cum.dose)) axis(1) axis(2,at=c(-6,-5,-4,-3,-2,-1,0,log10(10),log10(30),2), labels=c(expression(10^-6),quote(10^-5),quote(10^-4),quote(10^-3),quote(10^-2),quote(10^-1),1,10,30,100),las=1) box() dev.off()

12 February 2010

Ken Drake, Molecular Physiology SOM

• Ischemia will be induced in a portion of isolated rabbit hearts. Hearts are all healthy to begin with and several metabolites are measured in their healthy state once per minute. There are 6 types of ischemia groups, and hearts will be ischemic for 10 minutes. Each type of ischemia targets a different part of the metabolic process. Amino acid supplementation will occur pre-induction of ischemia.
• There are 14 groups (heathly+6 ischemia) and then these 7 are treated with amino acids and not treated with amino acids (7*2=14).
• It is vital that the baseline status of the hearts are quite similar.
• Some hearts may die during the experiment.
• Outcomes include the metabolite measures as well as an image of the beating heart. The beats will "break like a wave on the rocks" when it hits a dead portion. Images are recorded on the milisecond scale, metabolites measured once a minute. Possible differences are within the heart (ischemic area vs. healthy area) and between groups. Effects of ischemia on the healthy area are not clear.
• Needs a sample size and statistical analysis plan.

5 February 2010

Rachel Henry, Rheumatology

• Interested in showing the light chains expressed in the bone marrow are different than the light chains expressed in the spleen, which is the next step in the B-cell development. These light chains are the ones related to insulin-binding.
• For comparing between the two organs within a gene family, use a two-sample binomial test (or sometimes called the two-proportion test).
• For comparing between an organ and the possible catelog of light chains, a permutation test is a possibility.

22 January 2010

Kim Taylor, Cardiovascular Medicine

• Questions about kappa=NA or negative

Deanna Tzanetos, Pediatrics Critical Care Fellow

• Patients on cardiopulmonary bypass; found every patient within a year
• Main response variable is development of a clot
• Question about the use of mixed model
• A more appropriate approach might be a survival time analysis of time to clot
• Patients lost to follow-up before experience a clot are right censored at the last follow-up time
• If there are deaths "interrupting" the clot, these events are not independent of getting a clot and so present problems in the analysis and its interpretation
• Covariates are measured pre-op, postop day 1, 3, 5, q10d afterwords; last is post-op day 30
• Only 5 clotting events
• No modeling is feasible
• Upper limit on what might be analyzed reliably is a single baseline variable measured once
• For example, do a Cox model test of association of bypass time vs. time to clot (hazard of clotting)
• Only a descriptive study is possible
• Can do separate analyses of baseline and updated baseline data to study inter-relationships and redundancy of information
• Or use D-dimer or hematologic assessments as response variables

Nishitha Reddy, Hematology/Oncology

• Interested in getting data from the Synthetic Derivative
• May be good to consider creating a REDCap database

Adam Esbenshude, Pediatric Hematology/Oncology

• Pre-hypertension (using 90th percentile and z-scores)
• BP can be falsely elevated due to crying etc.
• Original idea to remove kids under 36m of age

15 January 2010

Nora Kayton and Rachel Reinert, Molecular Physiology & Biophysics graduate students

• 4 groups of mice by genotype
• Measured at multiple time points (baseline + 5 points)
• See http://biostat.mc.vanderbilt.edu/wiki/pub/Main/ClinStat/serialData.pdf for a summary statistic approach
• Also see http://biostat.mc.vanderbilt.edu/wiki/pub/Main/ClinStat/repmeas.PDF
• To normalize for the baseline value, it may be good to treat the baseline as a covariate
• A unified time-response model that can do this can be based on generalized least squares
• At some point it may be good to consider simultaneous confidence regions for differences between time-response curves
• Can model the time-response profile parametrically or using nonparametric regression (loess)
• Summary measure approach is the easiest; can feed this into an ANOVA (which makes strong normality and equal variance assumptions) or nonparametric ANOVA (Kruskal-Wallis test)
• Perhaps better is ANCOVA (analysis of covariance) to adjust for baseline

William Wolfle, Rheumatology Postdoral Fellow

• 3-5 mice from each genetic background; 3 groups
• RT-PCR
• Have 2 replicate measurements at 2 days
• Would be beneficial to show dot plots for the groups, with all raw data and with averaging over replicates
• Has been using a program called REST that uses a bootstrap technique to obtain P-values
• Found significant differences if don't normalize, non-significant if you do
• CD19 = B-cell marker gene; normalizer RNA; normalizes by division
• Need to think about what normalization really means
  • subtraction? division? subtract on the square root scale?
  • on raw data or average (geometric? arithmetic? median?) over replicates
• Assuming the ratio of CD19 and gene of interest is constant within a group
• Best to develop a unified model and not to assume that normalizing factors have no measurement error or biologic variability
• Come back, and send an email in advance to mailto:biostat-clinic@list.vanderbilt.edu to see if Dan Ayers can attend

8 January 2010

Peggy Kendall, Medicine (Allergy)

• Needed help responding to reviewer request for figure. Has a Kaplan-Meier curve from Renee, but data has no censoring; no need to go to special lengths to describe lack of censoring.

Kim Taylor, Medicine (Cardiology)

• Project involves two reviewers looking at 18 different patient education materials (PEMs), answering 28 different questions regarding content, layout, age appropriateness, etc. Examining reviewer agreement in preparation for writing manuscript and for creating a new PEM based on the best of the reviewed materials.
• Dan B. had suggested weighted kappa; we were unable to figure out how to do this in SPSS in a straightforward way, and suggested Kim email Dan B. for more help on that. ( SPSS documentation link) Also suggested looking at separate kappas for question groups (content, layout, graphics...) and possibly for each PEM, rather than one overall kappa.

• Bryan helped Kim compute some weighted Kappa scores using the kappa2 function in the irr library. This is the R code he used:

library(irr) setwd("Desktop") d<-read.csv("PEM.csv") kscore<-NULL for (i in 1:18) { m<-data.frame(rev1=d$Reviewer1[d$PEM==i],rev2=d$Reviewer2[d$PEM==i]) kscore[i]<-kappa2(m, weight="equal")$value }

This is the output

> kscore
[1] 0.6666667 0.4482759 0.7037037 0.6137931 0.8911917 0.7704918 0.5961538 [8] 0.5906433 0.9213483 0.4829545 0.5361446 0.4599407 0.4509804 0.4836066 [15] 0.4545455 0.6666667 0.3354430 0.5785953

• Kim also came to the Thursday clinic on 1/21 and we calculated two additional series of weighted kappa values for her. The R code and output is here. Kim.R

18Dec09

Robin Marjoram, Pathology

• Use non-parametric tests (Kruskal-Wallis and Mann-Whitney).
• Differences between multiple comparison adjusted tests and non-adjusted tests. It's OK to present results of both.
• non-parametric tests are good for outliers.

4Dec09

Uche Sampson, Cardiovascular Medicine

• Mice abdominal aorta diameters measured; interested in aneurysm
• 10 mice
• 3 measurement times per mouse, 4 regions, before and after sacrificing
• Can use an easy-to-interpret method: average absolute discrepancy (disagreement)
• Here there is only one measurement technique, and each mice has multiple measurements
• Measurements are not made quickly within mouse, allowing the technician to forget the previous measurement so as to start fresh
• All assessments of interest are intra-mouse
• Can compute mean absolute difference across mice, computing within-mouse |difference| at two different times
  • compute one number for each mouse, take simple average across 10 mice
  • can use bootstrap nonparametric percentile confidence intervals for the population mean discrepancy so as to not assume normality (and |differences| will not be normal)
• See http://biostat.mc.vanderbilt.edu/wiki/pub/Main/ClinStat/obsVar.pdf for background
• Bland-Altman plot is useful for ascertaining whether analysis of differences is on the correct scale (vs. transforming the diameters)
• Can compute a grand average over regions as well as region-specific estimates
• For longitudinal diameters can't do a discrepancy analysis but can compare long. with corresponding transverse measurements (using absolute differences)
• Frank will talk to Zhouwen

Renee Porier, Gen Int Med, Geriatrics

• Psychometrics issues
  • Refer to Warren Lambert or Ken Wallston

20Nov09

Matt Judson, Neuroscience

• 2-group mouse problem; one group has only 4 mice
• For one cell, use concentric circles and count number of dendritic branches within each ring
• Multiple measurements per neuron per mouse
• Also have multiple neurons
• Could do a redundancy analysis of the 4-12 rings to find out how many unique measurements there are, which will lead to a less conservative multiplicity adjustment
• Alternative is to use a curve fitting repeated measures approach and look for differences in shape
• Another alternative is to compute a summary index for each mouse and to compare two groups using a simple Wilcoxon-Mann-Whitney 2-sample rank-sum test
• The field has a tradition of treating multiple cells as independent observations, boosting N; not clear how independent they are
• General analysis would be a three-level mixed effects model (mouse, cell within mouse, radius within cell within mouse)
  • Number of mice may be too small for this
• Mentor: Pat Levitt; may qualify for VKC Stat & Methodology Core support; will bring up at today's core meeting

Emily Reinke, Warren Dunn, Sports Medicine

• Hop Test protocol
• One knee had surgery
• Typical analysis is average over 3 hops for each leg, then find ratio of averages for good:bad leg
• Tries to keep which leg is surgical blinded
• Data to date collected starting each patient on their right leg (N=69; will enroll additional N=200)
• Right vs left injuries about equal
• Found a learning effect across hops
• Examined interaction effect to see if learning is more pronounced in the bad or good leg
• Is "right" a de facto randomization?
• The group concluded that there is no compelling reason to randomize
• If leg dominance does matter (and the L:R dominance ratio is not too far from 1:1), then randomization is recommended

30Oct09

Brenda Jarvis, Pathology

• Mendelian inheritance in mice apparently not being observed in litter size frequency breakdown, perhaps due to a fatal genotype
• Suggested chi-square goodness of fit test
• Degrees of freedom equal to the number of "free" genotypes, which is one less than the number of unique genotypes
• http://surfstat.anu.edu.au/surfstat-home/tables/chi.php can be used to compute P-values (right tail areas)
• Another question: comparing litter sizes in knockout vs. wild types
  • Might consider Wilcoxon two-sample test or Kruskal-Wallis k-sample test
  • More general: regression model; can attempt to isolate "A" effect, "B" effect, etc.
  • Kruskal- Wallis used to test equality of 9 groups with one P-value

28Aug09

Dr. Maron, Cardiology

26Jun09

Shawn Garbett, Cancer Biology - sugar uptake in single cells

• Issue in weighting wells when they have differing numbers of cells
• In depleted group, one of the wells has a much different distribution
• Suggest blocking on well in an overall analysis; but main interest is in variability
• Major problem: variability is much greater in one well than the others; variability is not stable over wells
• Suggest making qqnorm plots by well by group to check for normality (tests for variance differences depend on this)
  • This is a test of adequacy of the log transformation
  • May need to solve for an optimal transformation
• Then get pooled variance estimates over wells (expanding the error degrees of freedom) and to a variance test between two groups at a time
• With more effort do quantile regression on log scale to model the 25th and 75th percentiles, which leads to a model of their difference (inter-quartile-range)
• Another alternative: bootstrap ratios of IQRs or variance to get a meaningful confidence interval for some variability comparison
• Goal: quantify intrinsic variability using as few transformations as possible

John Cleator, Cardiovascular Medicine

• Dogs and pigs: examining coronary artery blood flow and resistence with regard to protease receptor [CBF,CVR]
• A-dogs (young, healthy) and B-dogs (older)
• Acetylcholine used as control but found to be vasoconstricting in B-dogs
• Par-1 peptide posited to be vasoconstrictor independent of endothelium in dogs
• Pigs: opposide (vasodilation, increase CBF)
• CBF measured in proximal mid distal segments of CA
• Also measured at multiple concentrations of PAR1-AP (multiple measurements per dog but focus on measurements at the highest concentration of PAR1-AP)
• Need to know the number of dogs needed in each of two groups to reach a statistical goal
  • power [requires physiologic difference don't want to miss]
  • precision (margin of error; half width of confidence interval) [requires acceptable margin of error]
  • Need CBF to have a symmetric distribution and need an estimate of the SD at the highest conc.
• Acceptable margin of error: magnitude to which you want the group mean difference "nailed down"
• Baseline measurements will be ignored for now
• SD: pooled SD over A, B, concentration
• Data from the literature may be useful for assessing normality of CBF etc. (and possibility for getting better SDs)
• See https://data.vanderbilt.edu/biosproj/CI2/handouts.pdf for notes about margin of error and sample size calculations
• Planning pig studies: need an estimate of SD from previous studies, plus the acceptable margin of error

Another way of thinking

• Figure the number of animals that can be studied with the given budget
• Solve for the likely margin of error that the experiment will yield
• Or estimate the largest sample size needed and build in early stopping rules (group sequential testing)

19Jun09

Renee Porter, SOM; work with Bonnie Miller

• Moral distress in medical students caused by situations of their patients
• Survey with 3 sections; 104 questions (52 x 2 parts - how often/level of distress); also deals with burnout & coping; some sections added in last year
• Multiple errors in RedCap R download. Fixed syntax file, along with csv file, stored in ~/clinic/data

12June09

Sharon Phillips, Neurosurgery

• Question concerning randomization scheme

Dave Airey, Pharmacology

• Studying RNA frequency in a brain area in a mouse model
• How many sequences per animal are needed for a two group comparison?
• Esssentially, cluster sampling

5June09

Peggy Kendall, Department of Medicine

• Same study as previous week.
• Elizabeth showed her plots made.
• Discussed Type I error, Wilcoxon tests.

29May09

Peggy Kendall, Department of Medicine

• Comparing B-cell counts between knock out and wild type mice. Measurements of each type of cell are not repeated within a mouse.
• Reccommend using the Wilcoxon rank sum test to test for differences between groups. This non-parametric test is "immune" to the effect of outliers by testing the ranks instead of the means. (aka Mann-Whitney U test)
• Also reccommend a graphic that will show all points instead of the typical dynamite plot. Peggy will send her data to the biostat clinic page and we will create an appropriate graphic for Friday June 5.

# Elizabeth's Plot Code # 
stata.graph<-function(outcome=bcell$totalb, group=bcell$group, yname="Total B", yax=seq(min=2, max=12, by=2), txt.adj=0.1,
  label=c("btk-deficient", "btk-sufficient"),...){
  par(mar=c(2,6,2,3))
  plot(outcome~jitter(as.numeric(group), amount=0.1), xaxt="n", yaxt="n",
      pch=pts[as.numeric(group)], cex=size[as.numeric(group)], xlim=c(0.5, length(label)+.5),
      xlab="", ylab="", las=1, font=2, bty="L", ...)

      mtext(yname,2,  font=2, line=4, cex=2)
      axis(1, labels=label, at=c(1:length(label)), font=2, cex.axis=2, tick=FALSE, line=-0.5)
      axis(2, at=yax, font=2, cex.axis=2, las=1)

      segments(c(1:length(label))-0.25, by(outcome,group,median), c(1:length(label))+0.25, 
        by(outcome,group,median), col="black", lwd=2.5, lty="solid")

      text(1, max(outcome+txt.adj), paste("P = ",format(round(wilcox.test(outcome~group)$p.value, 3), nsmall=3), sep=""), cex=2)
}

bcell<-read.csv("C:\\Documents and Settings\\koehleea\\My Documents\\Clinic\\KendallPeggy\\bcell.csv", header=TRUE)
igg<-read.csv("C:\\Documents and Settings\\koehleea\\My Documents\\Clinic\\KendallPeggy\\Igg.csv", header=TRUE) 

pts<-c(19, 15) 
size<-c(1.25, 1)

pdf("C:\\Documents and Settings\\koehleea\\My Documents\\Clinic\\KendallPeggy\\graphs5.pdf", height=10, width=8)
   stata.graph(outcome=bcell$totalb, group=bcell$group, yax=seq(18, 32, 2), ylim=c(18,33), txt.adj=1,label=c("btk-deficient", "btk-sufficient"))
   stata.graph(outcome=bcell$totalfo, group=bcell$group, yax=seq(2,12,2), ylim=c(1,14), yname="Total Fo", txt.adj=1,label=c("btk-deficient", "btk-sufficient"))
   stata.graph(outcome=bcell$totalt2, group=bcell$group, yax=seq(2, 10, 2), ylim=c(1,12), yname="Total T2", txt.adj=1,label=c("btk-deficient", "btk-sufficient"))
   stata.graph(outcome=igg$igganti, group=igg$group, yax=seq(0, 1.4, 0.2), ylim=c(0,1.5), yname="Anti-Insulin IgG", txt.adj=0.1,label=c("btk-deficient", "btk-sufficient"))
   stata.graph(outcome=igg$iggtotal, group=igg$group, yax=seq(0, 1.4, 0.2), ylim=c(0,1.5), yname="IgG Total", txt.adj=0.1,label=c("btk-deficient", "btk-sufficient"))
dev.off()

• Plots for June 5

Beth Harrelson, Pediatrics

• Matched case control study to determine if intubation is related to secondary pulmonary hypertension in infants. The bigger question is when should infants be screened for seconary pulmonary hypertension, but this is something we can't really address with this study.
• Cases are in the hospital for around 8-12 months. Controls are infants matched for gestational age, but without secondary pulmonary hypertension. Two controls per case are matched retrospectively, with 64 controls and 32 cases. Female premies are more likely to make it, so gender was also matched on.
• Days to intubation ended is available.
• Descriptive statistics can be used to describe the patients at 30, 60 and 90 days, as well as the pulmonary hypertension diagnosis. Also describe the characteristics of the 4 that died. Limitations include not knowing the history of patients who are transferred to Vandy, or those who die before transfer could have occurred.

10April09

Carl Frankel, Peabody

• Studying stuttering at it's onset; emotions and language.
• Questions about his model and "interaction terms" or "joint effects".
• 19 kids who stutter, 22 who don't.
• Questions about shrinkage... recommend asking FrankHarrell.
• By what procedure do I get to a reasonable degree of shrinkage?

Lara Nyman, Endocrinology

• Measuring the speed of blood flow in mice in hypoglycemic and hyperglycemic states while imaging.
• 44 cases, less than 20 have survived both states
• If you ignore the "death issue", could use the surviving mice to do the following:
  • Calculate hypo-hyper
  • Create a variable marking which state came first, hypo or hyper
  • To test that the diff=0, create a linear model: diff ~ B0 + B1*order
  • Test for B0=0; if B0 > 0 then Hypo is faster than hyper
• Could test for differences in mice that lived and mice that died within the same state.
• Y_ij ~ B_0i + B_1*order_i + B_2*hyper_ij + e_ij
  • hyper - 0/1 (No/Yes)
  • order - 0/1 (Hypo last/First)
  • Y_ij - measurement
  • e - rror
  • still ignoring mice that died.
  • This is a mixed effects model.

3Apr09

Brian Lehmann and Chris Barton, Biochemistry

• Cells grown on a 12 well plate and each column was treated with a different dose of a drug. The number of surviving colonies in each well was determined.
• Wants to determine IC50 value which will describe the dose that will kill half of the cells.
• IC50 is typically calculated by the linear model that has log(% dead)~log(Dose), and IC50 is the log(dose that has 50% death expected.
• This is repeated across 10 cell lines for 1 drug. Needs a statistical test for IC50 between the cell lines.
• Sample size for t-test was performed using preliminary data, but the sd will be double checked.
• They work at the cancer center and will email Elizabeth or return to clinic.

27Mar09

Lisa Mace, clinical pharmacology

• Dividing by the baseline measurement to normalize - a big no no.
• Plot raw data (Apd90 on y, time on x) and examine if any transformation of the data (logarithm / square root / none) is necessary.
• Recover and record strip id / animal id
• Mixed models to take into account within-animal correlation.
• f(Apd90) ~ (f(baseline) + time ) * group, where f is the transformation of the data
• Summary-measurement approach (eg slope) is simple, but it may not be applicable (due to within-animal correlation)

06Feb09

Allison Martin, School of Medicine student

• Project in Liberia,assessing HIV/AIDS prevention programs
• Administering a 3 month follow-up study, education program
• Studying middle school students - some are older than normal due to war
• Outcome - effectiveness of course, how much knowledge have they retained/gained?
• Has a survey - multiple types of questions, most are TRUE/FALSE
• Roughly 150 control, 150 case
• Surveys are taken before the course, 3 months later and 9 months later
• May need to take into consideration type of school - cluster problem
• Suggest using regression model that adjusts for schools (a cluster variable), baseline scores and demographics with the outcome being the final score after course is given.
• Score - score of survey given.
• Mario - need a connection with somebody over there so project doesn't change once arrived.

16Jan09

Jeff Lemonick, Pediatric Endocrinology

• Studying 3 different diets (Protein, Fat, Carb) with normal weight and overweight children.
• Do normal and overweight kids secrete these particular hormones differently given different diets?
• Frank suggested making a graph with BMI percentile on the x-axis and the hormone on the y-axis and two different lines for normal and overweight children
• Could test the hypothesis that the slope=0 to test the adequacy that the group concept is ok
• Some children repeated, some didn't - need to give each child a consistent unique id.
• Can you come up with a question more general in nature than an "at this time" question?
• Wants to know if ghrelin drops after eating.
• Possibly use a slope or AUC measure, try to narrow your measure down to 1 summary number
• Emailed a series of Wilcoxon tests for baseline characteristics.

gut <- read.csv("gut.csv") gut <- upData(gut, w=as.numeric(weighttype), lowernames=TRUE)

sink("/tmp/z.txt") for(d in levels(gut$diet)) { cat('\n---------------------------------------\n',d, '\n') s <- spearman2(w ~ age + white + male + wt + wtper + wtsd + ht + htper + htsd + bmi + bmiper + bmisd + dxafat + glucose + insulin + homa + leptin + ghrelin + pyy, data=subset(gut, diet==d)) print(s) } sink("")

Paula McGown

• Health Risk Assessments survey
• Divided into two groups, wants to know if one group has a proportion with a risk factor than the other
• Specifically, "Do you smoke?" Answer: Yes/No
• Gender, age, Medical Center/University variables available
• Suggest logistic regression, adjusting for confounding variables such as age, gender, alcohol consumption, etc and include time variable. Time variable may not be linear.
• Measured over time on same individuals, large sample so probably don't need GEE to account for correlations
• Ordinal logistic regression (or proportional odds) suggested to model ordered factors such as (no smoking, 1 pack/week, 1 pack/day, ...)

09Jan09

Troy Apple

• Veterinarian needing a sample size analysis.
• Studying effects of an ointment in treating a tumor on mice
• Dichotomous: Either the mice stay the same/improve or get worse
• For 90% poweer, needed 51 mice.

Mark Rawls

10Feb06

Genie Moore

• They need to use a historical control due to budget issue. Would it be o.k. to use of historical control in animal study for secondary hypothesis testing?
• In general, it is not recommended to use a historical contorl. We should be very cautious when we use a historical control to avoid a possible bias due to the difference between populations.
• Considering that: (1) the study is a well controlled animal study; (2) the only condition which could be different will be tested using another control group (pregnant saline treated dogs) whether this condition affects the outcome of interest; and (3) the historical control will be used for the secondary hypothesis testing, it would be O.K. to use the historical control as long as they precisely specify it and are aware of the possible bias which might affect the conclusion to make.

Daniel Moore

• Is it better to do animal experiment within one day or spread over time?
• Unless they expect a day factor affects the outcome of interest or are interested in estimating day-to-day variability, it is better to do the experiment within one day since it would reduce variablity and more powerful.

Charlie Cox

• How to test whether several measurements would differ by gender and by left and right
• Since the measurements are repeatedly measured on each subject, the repeated ANOVA or a regression model was suggested to take into accout correlation

03Mar06

Peggy Kendall (Medicine)

• Compare clones generated from B lymphocytes invading pancreas of wild type versus transgenic mice
• Each sequence was categorized to one of 9 categories (the number of total categories is 19, but only 9 categories were observed for this data)
• The chi-square test for heterogeneity was initially considered. However, since there were several empty cells, Fisher's Exact test was suggested.

14 Apr 06

Olga Viquez and Kalyany Amarnath, Dept. of Pathology

• Animals sacrificed at 0,2,4,8 weeks
• Major interest is dose-response, i.e., association between sacrifice time and response (but watch out for steepening effect at 8 weeks)
• 4 responses which are counts
• Can analyze with proportional odds ordinal logistic model using likelihood ratio 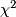test to handle heavy ties at zero count
• Analyze 4 types of counts separately
• Dataset should have one row per animal per organ with these columns: organ, time, 4 count variables (number of abnormal axons of different types)

Gaja Mahadeva (Postdoc, Surgery + BME)

• 7 points pre and post
• Reviewer made the mistake of requesting a correlation between pre and post (which could be perfect even if no experimental effect)
• Interested in experimental effect, not effect of baseline on response
• Suggested Wilcoxon signed-rank test
• Since all post < pre, doesn't matter whether analyze differences are ratios; 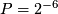(2-sided test)
• If any post were > pre would need to
  • Make Bland-Altman plots to determine whether differences, ratios, or some other measures are properly normalized for baseline
  • Use software to compute the Wilcoxon signed-rank test to handle compromises between + and - changes
• Could make a box plot of differences or log ratios (would need to justify the correct basis)
• Suppress right panel of the 2-panel graph in the manuscript; just show pre points connected to post points

Sam Oottamasathon (Pediatric Urology Fellow)

• Response is a count variable
• Compare treatment and control using Wilcoxon 2-sample rank test

21 Apr 06

Katie Stettler and Dale Edgerton (MPB)

• Problems with assumptions of repeated measures ANOVA
• Useful to analyze whole profiles, especially simultaneous confidence intervals for differences in profiles
• Gave handout on bootstrap technique making few assumptions
• Other possibilities: GEE, mixed effect models, generalized least squares
• Guess 15-30 hours of work for a single analysis; investment of significantly more time can result in a web-based tool for repeated use
• Minimize the need for normality assumption

Ute Schwarz and Mike Stein (Clin Pharm)

• 297 patient Warfarin study for a variety of indications
• INR treatment target range specific to indication related to bleeding potential
• Warfarin started empirically then titrated on basis of INR
• High inter-patient variability; some genotypes identified; cause differences in metabolism
• Primary question: effect of genotype on time to first INR within therapeutic range
  • Making basic assumption of no therapeutic "rescue" or other treatment change of major influence that can occur before INR ther. range hit (other than Warfarin dose adjustment)
  • Baseline covariates can be used to adjust for differing patient goals
• May be issue with physician variation in monitoring schedule for patient
• Important to model monitoring strategy as a function of baseline patient state to untangle potential nonuniformity of meaning of outcome measure
• Will present using INR, dose, and sensitivity index
• When gap in measurement, imputed between-measurement INRs
• Results will be overconfident because imputed values are treated as actual values (vs. multiple imputation)
• For subjects with long gaps in measurement times who were later found to have hit the therapeutic target, the time could be considered as left-censored
• Long gaps without hitting the target may be more ill-defined unless one assumes the target was never hit during the gap
• Cox proportional hazards model allows for baseline covariates; making assumption that effect of patient descriptors affects hazard of hitting target by a multiplicative amount
• Typically need 10 events per degree of freedom (e.g. number of covariates) in the model; current data has about 80% of 297 patients with an event

05May06

Peggy Kendall (Dept of Medicine)

• Compare the proportion of clones categorized in 14-111 clones to the proportions in the other categories
• Key issue: sparse data. Directed towards Fisher's Exact tests and Wilson Intervals for proportions.
• Created a spreadsheet for calculating Wilson Intervals and posted it in tools section at RobertGreevy.
• Followed up with an email of our recommendations and directions to the spreadsheet.

Matt Breyer (Dept of Medicine)

• Matt had done a number of analyses on his data, one of which was inconsistent with the others.
• We discussed why that analysis wasn't right for his data and the strengths of the other analyses.

17Nov06

Kristina Collins

Methotrexate to treat cutaneous lymphomas. n = 64 patients over a long period of time

1. two types of disease and some mixed
2. all patients belong to one doctor
3. we have the doctor's own data
4. All offered MTX - patient's choose whether or not to take.
5. more than half accepted - get exact count next time

Variables

1. outcome - time to progression (25% worsening of condition &/or transition to more serious cancer)
2. covariate - type of lymphoma, 2 groups and 2 hard pts hard to classify
3. outcome - treatment failure, noncompliance, disease progression, side effects, disease specific death
4. outcome - time to relapse, time from 1st complete response (total clearing of skin disease for 4+ weeks) to relapse
5. censoring - censor at last visit
   • need to look at actual visit frequency for pts.

• Really need a measure of disease status at time when offered MTX.
• Probably just drop the two pts that are mixed, i.e. hard to classify. 6 others have both skin diseases (LYP, PCALCL).

Timeline

1. Looking to finish in ~2 wks
2. Looking for paper to submit to Journal
3. Have a results sections
4. 2003 standford paper good guideline
5. next step - constructing table 1
6. bring laptop with data

Guoguang Rong

2 pictures to create.fixed date sometime last dec.

23Feb07

Jumy Fadugba

Allele protection effect on Harvard step test (physical fitnesss score, higher is better) controlling for number of episode per year on Diarrhea diseased children

1. APOE allele includes 4 or not
2. Only use the children followed for greater than 657 days
3. Wilcoxon rank sum test
4. Linear regression model

Api <- spss.get(file="Aptidao.sav") ApiSub <- Api[,c(1,2,16,32,33,34,36,37,38,39)] dat <- subset(ApiSub, OBSDAYS>657) dat$allele <- with(dat, ifelse(GENOTYP %in% c("2/4","3/4", "4/4"), 1,0)) with(dat, wilcox.test(allele, y=HSTSCORE)) dat$NUCYR <-dat$NOEPIS/dat$OBSDAYS*365 d <-datadist(dat) options(datadist="d") myfit <- ols(HSTSCORE ~ allele+NUCYR+allele*NUCYR, data=dat) myfit plot(myfit, NUCYR=NA,allele=NA,col=1:2)

18May07

Lance Eckerle, Pediatric ID

• Two groups of correlated measurements over generations of viruses
• Problem with measurements under the lower limit of detectability
• Can negate the response variable and treat as right-censored
• Can use summary statistic approach, fitting a right-censored linear regression separately for each curve
• Can use survreg in R survival package or psm in Design package with dist='gaussian'

x <- 1:5 y <- c(1,3,2,4,5) d <- c(1,1,1,1,0) plot(x, y) abline(lm(y ~ x)) g <- psm(Surv(y,d) ~ x, dist='gaussian') abline(g, col='red')

• See this handout for the summary statistic approach (but not handling censoring): STBRsylDesign

25May07

Design Studio for Kimberly Vera: Pulmonary Hypertension in Down Syndrome

• Major goal is to estimate the prevalence of PH in DS children
• For that purpose can do margin of error calculation

p <- seq(.02,.3,length=200) plot(p, 1.96*sqrt(p*(1-p)/50), type='l', ylab='Margin of Error', xlab='True Prevalence') lines(p, 1.96*sqrt(p*(1-p)/75), col='red') lines(p, 1.96*sqrt(p*(1-p)/100), col='blue')

• Suggest choosing DS sample size so that margin of error for prevalence is acceptable and the control sample size (lower than DS sample size) so that the margin of error of the most important mean chemical marker is acceptable
• For the latter need an estimate of standard deviation of the marker (or its log, dependingon the distribution) across children
• Margin of Error for Prevalence Estimation, n=50,75,100:
  

21Mar08

Peggy Kendall

• Cox model-logrank test for comparing two groups of mice
• Assume 50% reduction in probability of disease by 30w
• See http://en.wikipedia.org/wiki/Survival_analysis#Hazard_function_and_cumulative_hazard_function

cpower(30, 80, .7, 50, 0, 30)

Accrual duration: 0 y  Minimum follow-up: 30 y

Total sample size: 80

Alpha= 0.05

30-year Mortalities
     Control Intervention
        0.70         0.35

Hazard Rates
     Control Intervention
  0.04013243   0.01435943

Probabilities of an Event During Study
     Control Intervention
        0.70         0.35

Expected Number of Events
     Control Intervention
          28           14

Hazard ratio: 0.3578012
Standard deviation of log hazard ratio: 0.3273268
    Power
0.8809899

• Can also estimate the hazard ratio from existing data and get its 0.9 confidence interval; might use the least favorable confidence limit for the power calculation for a new study
• Often better to use biologic effects instead
• Need confidence bands of Kaplan-Meier curves or better, confidence intervals for differences
• Supplement with hazard ratio estimate and confidence limits

19Dec08

Sabina Gesell

• General Practitioner for Children's Hospital
• Doing a grant for a feasibility study concerning social networks and preventing childhood obesity.
• Recommended she find a statistician who does either social network modeling or spatial analysis - possibly somebody in sociology or psychology.

16Apr10

Peggy Kendall - Allergy Division, Dept. of Medicine

• B-cells, treated vs. non-treated
• Y= # mutations
• About 6 animals; used multiple mice to get enough volume for samples
• Pooled samples; sample = inflamed pancreas islets
• Don't example samples from same mouse to be more similar to each other than samples from two different mice
• Good options: Poisson or proportional odds two-sample problem; Poisson is sometimes said to be more appropriate when the counts are bounded
• A large P-value would be interpreted as there being insufficient evidence for a difference; one may not conclude that there is no difference
• Best to use confidence limits; for Poisson, this would be in terms of relative risk of a CDR mutation in one treatment group over another, or in terms of the ratio of two means (anti-log of Poisson regression coefficient)

<highlight> yuntreated <- c(rep(0,29), rep(1,6), rep(2,8), rep(3,1), rep(8,1)) ytreated <- c(rep(0,19), rep(1,4), rep(2,2), rep(3,2), rep(4,1), rep(5,1)) treat <- c(rep('untreated', length(yuntreated)), rep('treated', length(ytreated))) y <- c(yuntreated, ytreated) cbind(treat, y) tapply(y, treat, mean) # treated untreated #0.7931034 0.7333333 #tapply(y, treat, var) # treated untreated # 1.884236 1.972727 # Means and variances appear dissimilar # Use negative binomial model require(MASS) f <- glm.nb(y ~ treat) f summary(f) # Coefficients: # Estimate Std. Error z value Pr(>|z|) # (Intercept) -0.23180 0.34601 -0.670 0.503 # treatuntreated -0.07835 0.44627 -0.176 0.861 exp(coef(f)[2]) exp(coef(f)[2] + c(-1,1)*1.96*.44627) # treatuntreated # 0.9246377 # [1] 0.3855661 2.2174012 95% confidence limits for ratio of means </highlight> So the data are consistent with a doubling and a halving of the number of mutations due to the treatment.

Current Notes