You are here: Vanderbilt Biostatistics Wiki>Main Web>Education>HandoutsBioRes>JournalClubs>JournalClubNephrology>ReviewTepel04 (08 Nov 2004, FrankHarrell)Edit Attach
Review of Tepel et al, NEJM 2000;343:180-4
Biostatistical Reviewer: FrankHarrell
This paper demonstrates that even in a premier journal, statistical reviews are frequently inadequate. Fortunately, the authors got the right answer to their questions, but had the results been "non significant", the use of inefficient and inappropriate analyses would have been the cause.Minor Problems
- Table 1 shows the mean, standard deviation, and percentages of various baseline variables stratified by treatment. Means and SDs are poor descriptive statistics for asymetrically distributed variables. Quartiles are far better. And there is no need to stratify by treatment in a randomized trial. Apparent baseline imbalances would have been misleading and would have been counterbalanced by baseline characteristics omitted from Table 1. Table 1 should have thus included only one column. Much more valuable would have been a table or graphic containing patient responses stratified by levels of baseline variables. Who is having contrast-agent-induced reductions in renal function?
- The authors use improper nomenclature. On the bottom right of P. 181 the authors use the term "relative risk". It is not clear whether this is actually "odds ratio". Odds ratios are preferred (and should be labeled correctly) as they can apply to high- as well as low-risk patients. Odds ratios arise from logistic regression modeling.
- In a parallel-group randomized trial design, comparisons of major interest are always between treatment arms. In a few places the authors have slightly overemphasized changes over time within patients. Regression to the mean and natural history can make such changes difficult to interpret.
Major Problems
Dichotomization of Renal Function Measure
- The authors analyzed the effect of acetylcysteine on restoration of renal function after use of radiographic contrast agents for patients with renal dysfunction (serum creatinine > 1.2 mg/dl) undergoing CT. The authors made a common mistake in trying to categorize a continuous variable, which requires an arbitrary cutpoint to be used, results in a major loss in power, and is prone to problems with measurement errors. An artificial construct "acute contrast agent-induced reduction in renal function" was defined as an increase in creatinine (cr) of at least 0.5 mg/dl 48h after administration of the contrast agent. Besides the serious statistical problems listed above, this procedure suffers from the fact that cr does not "work" on a simple difference scale (see below).
- To make matters worse, the authors used Fisher's exact test after dichotomizing cr change. This test is conservative (loses power) as compared to the ordinary Pearson chi-square test.
Incorrect Adjustment Variables in Logistic Regression Analysis
- The authors used multiple logistic regression to analyze the binary response of acute reduction. Besides the general and particular problems of dichotomizing cr indicated above, the authors adjusted for the wrong variables. They adjusted for baseline blood pressure while also having treatment in the model. It is mandatory to adjust for baseline renal function, which we expect to be a strong predictor in general but especially when the inappropriate change score was chosen. The model needs to compensate for the fact that those with larger baseline cr are easier to change by a fixed absolute amount (0.5 mg/dl). Adjustment for the baseline version of response variables will always increase power. Adjustment for cause of renal insufficiency may also be warranted.
Wrong Scale for Quantifying Effects (Differences)
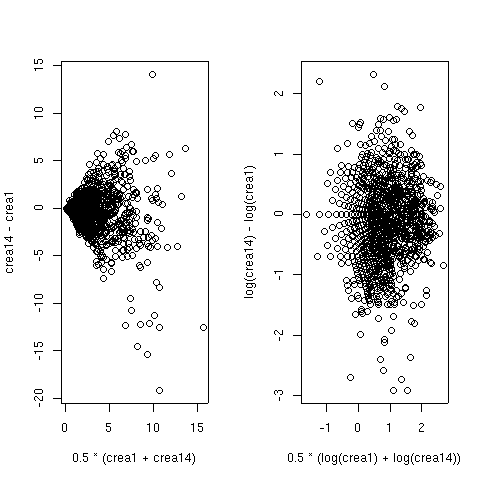
As discussed above, it is important to analyze patient responses in a way that does not destroy information. Serum cr should be used as a continuous variable, which fortunately the authors did for some of their analyses. But whether computing change over time within patient or difference in group means across the parallel treatment arms at a single time, it is important to choose the correct transformation of the response variable before taking differences. There are at least three ways to find the best transformation of cr:- Find the transformation so that a difference between transformed values has no relationship between the average of the two transformed values (Bland-Altman plot). This is a way to demonstrate that the change measure is independent of baseline.
- Find the transformation so that transformed crs have equal variability across levels of other important variables (e.g., etiology, baseline cr, age). This makes the transformed values satisfy usual multiple regression assumptions.
- Find the transformation that makes serum cr linearly related to log odds of short-term death or, when follow-up is long, of log hazard of death. In the case of cr and other lab parameters (the most common situation of interest is a parameter such as white blood count that has a two-sided normal range), the transformation of the parameter that makes it optimally predict death is not monotonic (e.g., very low and very high values can achieve the same mortality risk). There may be a need to analyze changes in the parameter after making such a complex transformation to a "risk score" scale.
To try method 2 on the same dataset, we first stratify patients by intervals of day 1 cr (
crea1) having 100 patients per interval. Within each interval the quartiles (25th and 75th percentiles and the median) of cr at day 14 (crea14) are plotted against the mean crea1 in the interval. Results are shown below.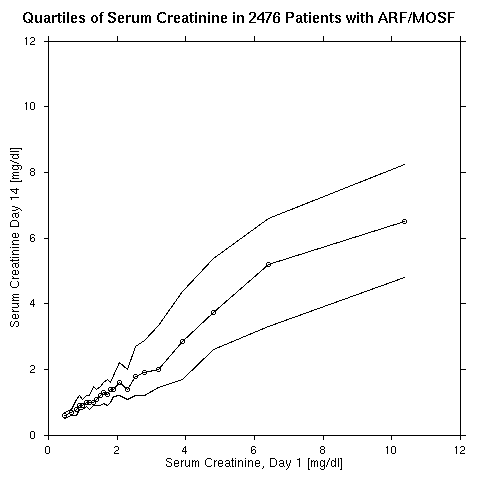
It is easy to see that variability of
crea14 increases with crea1. It is easy to "move" cr when it is already large. The authors confirm this in their nice figure 1 but do not act accordingly. Next, a nonparametric regression model called AVAS (additivity and variance stabilization) was used. This methods solves for optimum transformations in crea1 and crea14 that maximizes their linear correlation coefficient while making the variance in crea14 as stable as possible across levels of crea1. The estimated transformations and their confidence intervals follow.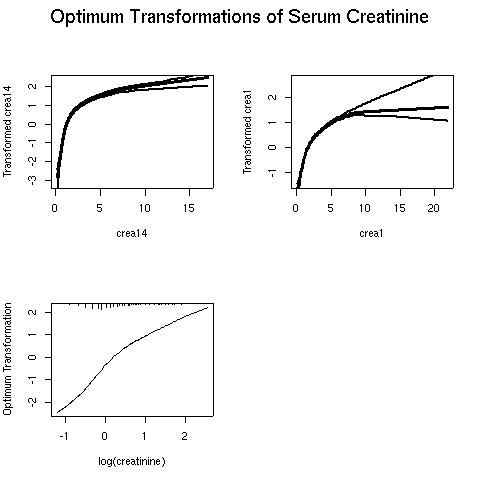
These transformations are almost logarithms. The bottom left panel shows how close the optimum transformation is to a log. A straight line would indicate that log was perfect. Stratified quartiles of
crea14 against intervals of crea1 are shown below but using the optimum transformed transformation for crea14.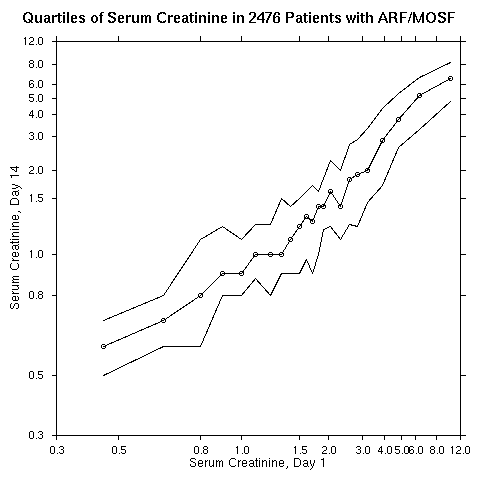
Variability is much more constant across the whole range of
crea1.
Improved Primary Analysis
The suggested analysis is to use analysis of covariance to predict optimum transformed post-treatment cr from the following baseline variables: treatment, transformed baseline cr, mean arterial blood pressure, and cause of renal insufficiency. If the log transformation is used, the antilog of the regression coefficient for treatment estimates the ratio of the population medians of final cr for those receiving the new treatment compared to control patients, adjusted for the other variables. In this parallel-group design this ratio is also the ratio of ratios of final to baseline cr when comparing treated and control for the same baseline value of cr. For any transformation, one can use the fitted model to estimate the median post-treatment cr for each treatment, and the difference between treatments on the original scale for any pre-treatment cr. Only for the (incorrect) linear transformation will this difference not depend on the initial cr.| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
creatinine.s | manage | 1 K | 08 Nov 2004 - 22:08 | FrankHarrell | S code used to analyze SUPPORT data and graph data |
| |
creatinine1.png | manage | 4 K | 08 Nov 2004 - 22:07 | FrankHarrell | |
| |
creatinine2.png | manage | 5 K | 08 Nov 2004 - 22:07 | FrankHarrell | |
| |
creatinine3.png | manage | 8 K | 07 Nov 2004 - 05:59 | FrankHarrell | Altman-Bland plots |
| |
creatinineOptimum.png | manage | 4 K | 06 Nov 2004 - 08:25 | FrankHarrell |
Edit | Attach | Print version | History: r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r3 - 08 Nov 2004, FrankHarrell
 Copyright &© 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright &© 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Vanderbilt Biostatistics Wiki? Send feedback