You are here: Vanderbilt Biostatistics Wiki>Main Web>Projects>MicroArrayMassSpec>GeneralWfccmDesign>WfccmClassDescriptions>WfccmAlgorithmSAM (revision 11)EditAttach
SAM Algorithm
The data is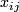 , i = 1, 2, ... p genes, j = 1, 2, ... n samples, and response data
, i = 1, 2, ... p genes, j = 1, 2, ... n samples, and response data Generic SAM procedure :
- Compute a statistic :
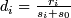 ; i = 1, 2, ... p
; i = 1, 2, ... p -
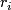 is a score.
is a score.
-
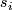 is a standard deviation.
is a standard deviation.
-
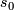 is a fudge factor.
is a fudge factor.
-
Details of 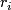 and
and 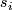 for Two Class, Unpaired Data response type :
for Two Class, Unpaired Data response type :
-
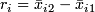
-
 .
.
-
 .
.
-
-
![$s_i = [(1/n_1+1/n_2)\{\sum\limits_{j \in C_1}^{} (x_{ij} - \bar x_{i1})^2 + \sum\limits_{j \in C_2}^{} (x_{ij} - \bar x_{i2})^2\}/(n_1+n_2-2)]^{.5}$](/wiki/pub/Main/WfccmAlgorithmSAM/latex6723ab1600bf747a93d613e764d34221.png)
-
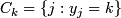 ; k = 1,2.
; k = 1,2. 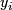 = 1 or 2.
= 1 or 2.
-
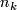 is the number of observations in
is the number of observations in 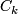 .
.
-
Computation of 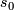 :
:
- Compute the 100 quantiles of the
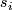 values, denoted by
values, denoted by 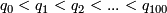 .
.
- For
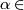 (0, .01, .02, ... 1.0)
(0, .01, .02, ... 1.0) - Let
 , where
, where 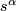 be the
be the 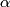 percentile of the
percentile of the 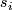 values.
values.
- Compute
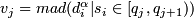 , j = 1, 2, ... 100, where _mad_ is the median absolute deviation from the median, multiplied with 1.4826.
, j = 1, 2, ... 100, where _mad_ is the median absolute deviation from the median, multiplied with 1.4826.
- Compute cv(
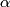 ) =
) = 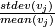 .
.
- Let
- Choose
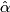 = argmin[cv(
= argmin[cv(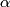 )].
)].
- Finally compute
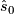 =
= 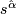 .
. 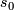 is henceforth fixed at the value
is henceforth fixed at the value 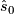 .
.
Topic revision: r11 - 13 Sep 2005, ColeBeck
 Copyright © 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © 2013-2022 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Vanderbilt Biostatistics Wiki? Send feedback