Determinant of a matrix

Determinants palys an important role in finding the inverse of a square matrix and also in solving systems of linear equations.

Determinant of a 2*2 matrix

Assuming A is an arbitrary 2*2 matrix A, where the elements are given by:
A = {{,},{,}}
then the determinant of a this matrix is as the follows:
det(A) = |A| = |{,},{,}| = -

Determinant of a 3*3 matrix

The determinant of a 3*3 matrix is found as follows
A = {{,,},{,,},{,,}}

then the determinant of a this matrix is as follows:
det(A) = |A| = |{,,},{,,},{,,}|
= |{,},{,}|-|{,},{,}|+|{,},{,}|

Determinant of a n*n matrix

For the general case, where A is an n*n matrix the determinant is given by:
det(A) = |A| = ++...+
Where the coefficients are given by the relation
=
where is the determinant of the (n-1)*(n-1) matrix that is obtained by deleting row i and column j. This coefficient is also called the cofacotr of

Minor of a matrix

A minor of a matrix is the determiniant of a certain samller matrix. Suppose A is an m*n matrix and k is a positive integer not larger than m and n. A k*k minor of A is the determinant of a k*k matrix obtained from A by deleting m-k rows and n-k coulmns.
example:
given the matrix A = {{1,4,7}{3,0,5}{-1,9,11}}
the minor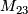 of A is
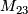= {{1,4}{-1,9}}

Adjoint of a matrix

Adjoint matrix can be calculated by the following method

• Given the n*n matrix A, define
  B = ()

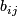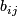to be the matrix whose coefficients are found by taking the determinant of the (n-1)*(n-1) matrix obtained by deleting the ith row and jth column of A. The terms of B(i.e. B = ) are known as the cofactors of A.

• And define the matrix C, where
  
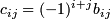
• The transpose of C is called the adjoint of Matrix A.